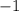7–10. Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней. Решаем уравнения, находим корни уравнения и сравниваем ответы.
7. 1)
число в корне не может равняться отрицательному числу, корней уравнения нет.
2)
число в модуле не может равняться отрицательному числу, корней уравнения нет.
=> уравнения равносильные.
8. 1)
корней уравнения нет.
2)
корней уравнения нет.
=> уравнения равносильные.
9. 1)
ОДЗ: , ;
(не удовлетворяет ОДЗ),
ответ:
2)
,
ответ: ;
=> уравнения не равносильные.
10. 1)
ОДЗ: , ;
ответ:
2)
ответ:
=> уравнения равносильные.
12–16. Необходимо найти сумму корней уравнения. Решаем уравнение, находим корни уравнения, складываем их. Если уравнение имеет один корень, то суммой (ответом) будет значение корня уравнения.
В решении.
Объяснение:
2. Найдите периметр фигуры. ответ запишите в виде многочлена стандартного вида и укажите его степень.
Памятка:
Как найти сумму и разность многочленов и записать результат как многочлен стандартного вида.
1) Записать многочлены в одну строку, второй многочлен в скобках, между ними знак + или -.
2) Раскрыть скобки. Если между многочленами знак +, во втором многочлене знаки не меняются, если перед скобками знак -, меняются на противоположные.
3) Привести подобные члены.
4) Записать результат в стандартном виде, т.е., в порядке убывания степеней и в алфавитном порядке.
Так как при нахождении периметра выполняется сложение многочленов, можно сразу записать сумму, без скобок.
ху² + 5 + 4ху - 3ху² + 2х² + 4ху =
= -2ху² + 2х² + 8ху + 5.
Степенью многочлена называется наибольшая из степеней его слагаемых.
Степень многочлена (ху²) = 3.
7–10. Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней. Решаем уравнения, находим корни уравнения и сравниваем ответы.
7. 1)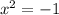
число в корне не может равняться отрицательному числу, корней уравнения нет.
2)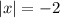
число в модуле не может равняться отрицательному числу, корней уравнения нет.
=> уравнения равносильные.
8. 1)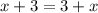
корней уравнения нет.
2)
корней уравнения нет.
=> уравнения равносильные.
9. 1)
ОДЗ: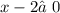 ,
, 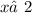 ;
;
ответ: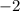
2)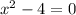
ответ: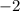 ;
; 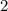
=> уравнения не равносильные.
10. 1)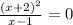
ОДЗ: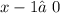 ,
, 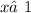 ;
;
ответ: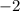
2)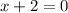
ответ: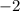
=> уравнения равносильные.
12–16. Необходимо найти сумму корней уравнения. Решаем уравнение, находим корни уравнения, складываем их. Если уравнение имеет один корень, то суммой (ответом) будет значение корня уравнения.
12.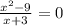
ОДЗ: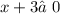 ,
,  ;
;
ответ: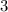
13.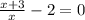
ОДЗ: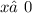 ;
;
ответ: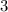
14.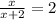
ОДЗ: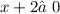 ,
,  ;
;
ответ: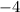
15.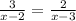
ОДЗ: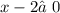 ,
, 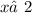 ,
, 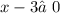 ,
, 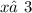 ;
;
ответ:
16.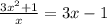
ОДЗ: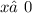 ;
;
ответ: