Алгебра: ЛЕГКИЕ ЗАДАНИЯ ПО АЛГЕБРЕ НА

ЛЕГКИЕ ЗАДАНИЯ ПО АЛГЕБРЕ НА

Показать ответ

Ответ:

olgamaryutina

10.12.2020 12:28

Объяснение:

9 . . . . = [ ( x - 3y )( x + 3y ) * ( a + b )( a + 4b )]/[ ( a + 4b )² * ( 3y - x ) ] =

= [ - ( x + 3y ) ( a + b )/( a + 4b ) .

10 . . . . . . . . . . . . . . . . . . . .

[ 5² - ( a² + 2ab + b²) ]/[ ( a² - 5² ) + ( ab + 5b ) ] = ( 5 + a + b )/x ;

[ 5² - ( a + b )² ]/[ ( a - 5 )( a + 5 ) + b( a + 5 ) ] = ( 5 + a + b )/x ;

[ (5 - a - b ) ( 5 + a + b ) ]/[ ( a + 5 )( a - 5 + b ) ] = ( 5 + a + b )/x ;

- 1 / ( a + 5 ) = 1 /x ;

x = ( a + 5 )/( - 1 ) = - ( a + 5 ) ; x = - ( a + 5 ) .

0,0(0 оценок)

Ответ:

НикСол

31.01.2021 07:09

Задача. Сколько действительных корней имеет уравнение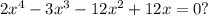 $2x^{4} - 3x^{3} - 12x^{2} + 12x = 0?$

Укажите интервал, которому принадлежит наименьший корень:

$1) ~ (-4; ~ {-}3);\\2) ~ (-3; ~ {-}2);\\3) ~ (-2; ~ {-}1);\\4) ~ (1; ~ 2);\\5) ~ (2; ~ 3).$

ответ запишите в виде: k, ~ m, где 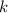— число корней, 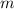— номер промежутка, которому принадлежит наименьший корень.

Решение. Вынесем общий множитель за скобки:

$x(2x^{3} - 3x^{2} - 12x + 12)=0.$

Произведение множителей равно нулю тогда, когда хотя бы один из них равен нулю:

1) ~ x = 0;

$2) ~ 2x^{3} - 3x^{2} - 12x + 12 = 0.$

Видя последнее уравнение, понимаем, что искать все его корни не нужно. Этого и не требуют в задании.

Рассмотрим функцию $f(x) = 2x^{3} - 3x^{2} - 12x + 12.$

1) Область определения: $D(f) = (-\infty; ~ {+}\infty).$

2) Исследуем данную функцию на четность:

$f(-x) = 2(-x)^{3} - 3(-x)^{2} - 12(-x) + 12 = -2x^{3} - 3x^{2} + 12x + 12 =\\= - (2x^{3} + 3x^{2} - 12x - 12) \neq -f(x).$

Функция не обладает свойством четности. Она ни четная, ни нечетная.

3) Определим нули функции.

3.1. Пересечение с осью $x \colon$

$2x^{3} - 3x^{2} - 12x + 12 = 0.$

Невозможно дать точный ответ.

3.2. Пересечение с осью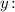 $y \colon$

$2 \cdot 0^{3} - 3\cdot 0^{2} - 12\cdot 0 + 12 = 12.$

Значит, (0; ~ 12) — точка пересечения с осью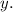

4) Найдем производную функции:

$f'(x) = 6x^{2} - 6x - 12.$

5) Определим критические точки функции, приравняв производную к нулю:

$6x^{2} - 6x - 12 = 0 ~~~ |: 6$

$x^{2} -x - 2 = 0$

$x_{1} = -1; ~ x_{2} = 2$

Определим точки экстремума и экстремумы функции:

$f' ~~~~~ + ~~~\max~~~~~ - ~~~~\min~~~+\\------|------|-----x\\f ~~~~~\nearrow~~~~ {-}1 ~~~~~~\searrow~~~~~~ 2~~~~~ \nearrow$

Итак:

$x_{\max} = -1; ~~~ x_{\min} = 2.$

$y_{\max} = 2 \cdot (-1)^{3} - 3 \cdot (-1)^{2} - 12 \cdot (-1) + 12 = 19$

$y_{\min} = 2 \cdot 2^{3} - 3 \cdot 2^{2} - 12 \cdot 2 + 12 = -8$

6) Изобразим схематически график функции, строго соблюдая все найденные точки, монотонность функции и симметрию линий около критических точек (см. вложение).

Выводы. Как видно из графика, из уравнения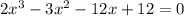 $2x^{3} - 3x^{2} - 12x + 12 = 0$ имеем три действительных корня, наименьший из которых находится в интервале 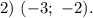2) ~ (-3; ~ {-}2). Таким образом, уравнение 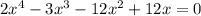$2x^{4} - 3x^{3} - 12x^{2} + 12x = 0$ имеет четыре действительных корня.