Задание: разложить на множители. множители - компоненты при умножении ⇒выражение представляет собой произведение многочленов. преобразовать данное выражение так, чтобы в каждом слагаемом были одинаковые множители. 1. m-n+p(m-n). 3-е слагаемое состоит из двух множителей р и (m-n), значит первое и второе слагаемое группируем и записываем (m-n). необходимо представить в виде произведения двух множителей. один множитель (m-n), второй множитель в этом слагаемом может быть только 1. получаем: m-n+p(m-n)=(m-n)*1+p*(m-n)=(m-n)*(1-p)
1) для того чтобы функция была непрерывной, нужно чтобы пределы слева и справа в точках 0 и 1 были равны. Найдем их:
Так как 1≠-∞, то точка 0- это точка разрыва(второго рода).
Чтобы функция была неразрывной в точке 1, нужно чтобы предел от 3-ax^2 был равен 2, так как
При x=1 ⇒y=2.
Подставим координаты (1;2) в формулу y=3-ax^2⇒2=3-а⇒а=1, то есть уравнение имеет вид y=3-x^2. Проверим это: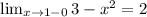
Действительно 2=2, значит функция не будет являться непрерывной в точке 1.
ответ: х=0 - точка разрыва. функция непрерывна в точке х=1 при а=1
2) Аналогично:
3≠-1, значит -1- это точка разрыва.
В точке x=1 ⇒y=1. Подставим: 1=a*1⇒a=1.
Проверим: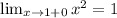 .
.
Так как точка х=0 лежит в области определения функции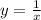 , а из ОДЗ следует что х≠0, то функция также будет прерываться в точке х=0
, а из ОДЗ следует что х≠0, то функция также будет прерываться в точке х=0
ответ: х=-1 - точка разрыва, х=0- точка разрыва, функция будет непрерывна в точке х=1 при а=1
множители - компоненты при умножении ⇒выражение представляет собой произведение многочленов.
преобразовать данное выражение так, чтобы в каждом слагаемом были одинаковые множители.
1. m-n+p(m-n). 3-е слагаемое состоит из двух множителей р и (m-n), значит первое и второе слагаемое группируем и записываем (m-n). необходимо представить в виде произведения двух множителей. один множитель (m-n), второй множитель в этом слагаемом может быть только 1. получаем:
m-n+p(m-n)=(m-n)*1+p*(m-n)=(m-n)*(1-p)
4q(p-1)+p-1=4q*(p-1)+(p-1)*1=(p-1)*(4q+1)
4q(p-1)+1-p=4q*(p-1)-1*(p-1)=(p-1)*(4q-1)