лоторея билеті сатылған. Оларда 500 тг-ден бір ұтыс, 100 тг-ден он ұтыс, 50 тг-ден елу ұтыс бар, ал қалған билеттерде ұтыс жоқ. Бір лоторея билетін сатып алған адам үшін ұтыстың үлестірім заңын табыңдар.
Предположим, что утверждение верно для n=k. Покажем, и докажем, что утверждение верно так же для n=k+1. Так как , следуя предположению то прибавив к данному выражению d. Мы получим следующий член . Т.е. предположение верно. Ч.Т.Д.
2) База : 1 Проверка: .
Предположение:
Теперь покажем и докажем, что данное выражение верно и при :
Так как предыдущий член был равен k, то что бы узнать сумму первых k+1 членов, достаточно прибавить k+1 член (используя формулу которую мы доказали ранее): т.е. мы пришли к изначальной формуле, если туда подставить k+1. Ч.Т.Д.
3) Это не формула общего члена, это формула суммы. При получается деление на ноль, поэтому сразу пишем База: 1 Предположим, что формула верна для: Покажем и докажем что формула верна для : Как и с суммой арифм.прогрессии. Мы добавим k+1 член к сумме. Ч.Т.Д.
1) Используя формулу n-го члена арифметической прогрессии , вычислим двадцатый член этой прогрессии:
ответ: 30.
2) Формула суммы первых n членов арифметической прогрессии следующая:
Найдем же сначала восемнадцатый член арифметической прогрессии
ответ: 656.
3) Первый член:
Второй член:
Третий член:
Как видно, каждый последующий член уменьшается на (-5),т.е. это разность d = -5, следовательно, последовательность является арифметической прогрессией.
4) Используя n-ый член арифметической прогрессии, найдем ее разность
Да, является арифметической прогрессией.
5) Данная последовательность является арифметической прогрессии с первым членом и разностью прогрессии d=1
Всего таких членов не трудно посчитать по формуле n-го члена арифметической прогрессии:
То есть, нужно посчитать сумму первых 91 членов арифметической прогрессии
База индукции: 1
Предположим, что утверждение верно для n=k.
Покажем, и докажем, что утверждение верно так же для n=k+1.
Так как , следуя предположению
Т.е. предположение верно. Ч.Т.Д.
2)
База : 1
Проверка:
Предположение:
Теперь покажем и докажем, что данное выражение верно и при
Так как предыдущий член был равен k, то что бы узнать сумму первых k+1 членов, достаточно прибавить k+1 член (используя формулу которую мы доказали ранее):
т.е. мы пришли к изначальной формуле, если туда подставить k+1. Ч.Т.Д.
3)
Это не формула общего члена, это формула суммы.
При
База: 1
Предположим, что формула верна для:
Покажем и докажем что формула верна для
Как и с суммой арифм.прогрессии. Мы добавим k+1 член к сумме.
Ч.Т.Д.
1) Используя формулу n-го члена арифметической прогрессии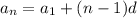 , вычислим двадцатый член этой прогрессии:
, вычислим двадцатый член этой прогрессии:
ответ: 30.
2) Формула суммы первых n членов арифметической прогрессии следующая: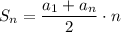
Найдем же сначала восемнадцатый член арифметической прогрессии
ответ: 656.
3) Первый член: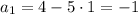
Второй член: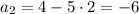
Третий член: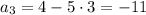
Как видно, каждый последующий член уменьшается на (-5),т.е. это разность d = -5, следовательно, последовательность является арифметической прогрессией.
4) Используя n-ый член арифметической прогрессии, найдем ее разность
Да, является арифметической прогрессией.
5) Данная последовательность является арифметической прогрессии с первым членом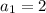 и разностью прогрессии d=1
и разностью прогрессии d=1
Всего таких членов не трудно посчитать по формуле n-го члена арифметической прогрессии:
То есть, нужно посчитать сумму первых 91 членов арифметической прогрессии
ответ: 4277.