Маємо кошик із цукерками різних видів, у якому 7 цукерок — «Буревісник», 3 цукерки — «Полуничні» і 12 цукерок — «Білочка». Визнач, скількома можна вибрати 3 цукерки так, щоб це були 1 «Буревісник», 1 «Полунична» і 1 «Білочка».

находим уравнение стороны AB:

A(7;9); B(9;-6)

уравнение прямой на плоскости через две точки:

Подставим координаты точек:

приведем уравнение к виду y=kx+b:

угловой коэффицент данной прямой:

k=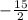

Если у прямых равны угловые коэффициенты, то они параллельны.

Составляем уравнение прямой с угловым коэффициентом k=-15/2 и проходящую через точку C(8;10)

Находим уравнение стороны BC:

Находим точку пересечения прямых y+16x-138=0 и 2y+15x-140=0:

Прямая 2y+15x-140=0 пересекается с BC в точке C и параллельна стороне AB=>  эта прямая касается треугольника ABC в точке C, и ее длина в этом треугольнике равна нулю.

1) 2y+15x-140=0

2) L=0

Объяснение:

При умножении одночлена на многочлен, выполняется распределительное свойство умножения:

a*(b+c)=a*b+a*c;

(a-b)*c=a*c-b*c;

Для того чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить полученные произведения.

Пример:

Выполним вычисление выражения двумя

1) Прямой

Сначала выполняем действие в скобках, затем умножение.

5-2=3

3*4=12.

2) С свойства

Воспользуемся распределительным свойством:

(5-2)*4=5*4-2*4 = 20-8=12

С одночленами и многочленами всё то же самое.

a*(b+c)=ab+ac;

4a²(b²+bc+c²)=4a²*b²+4a²*bc+4a²*c².