1) было у Бори;
2) 896(цветов) - было на празднике;
3) среднее арифметическое - 36
мода ряда - 121
размах ряда - 182
Объяснение:
1) Сейчас у Бори 160 руб(100%-95%).
160/0,95=16000/95= (руб) было у Бори.
2)100% -75%=25% георгинов было на празднике
224 25%
? 100%
(224*100)/25=224*4=896(цветов) - было на празднике.
3)
среднее арифметическое(сумма всех членов ряда, деленная на их количество) - (15+121-61+121+0+20)/6=36
мода ряда (число, которое в ряду встречается чаще других) - 121
размах ряда (разность наибольшего и наименьшего чисел) - 121-(-61)=182
1. Область определения: На ноль делить нельзя --> и х не отрицательный т.к. х под натуральным логарифмом. Итоге: x∈[0;1)∪(1;+∞)
2. Функция общего вида т.к. f(-x)≠±f(x)
3. Точки пересечения с осями:
Только одна точка (0;0)
4. Исследование с 1ой производной:
см. внизу.
5. Исследование со 2ой производной:
6. Асимптоты:
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:
Находим коэффициент k:
Находим коэффициент b:
Предел равен ∞, следовательно, наклонные асимптоты функции отсутствуют.
Найдем вертикальные асимптоты. Для этого определим точки разрыва:
Находим переделы в точке 1:
Значит точка разрыва II рода и является вертикальной асимптотой.
1)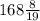 было у Бори;
было у Бори;
2) 896(цветов) - было на празднике;
3) среднее арифметическое - 36
мода ряда - 121
размах ряда - 182
Объяснение:
1) Сейчас у Бори 160 руб(100%-95%).
160/0,95=16000/95=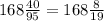 (руб) было у Бори.
(руб) было у Бори.
2)100% -75%=25% георгинов было на празднике
224 25%
? 100%
(224*100)/25=224*4=896(цветов) - было на празднике.
3)
среднее арифметическое(сумма всех членов ряда, деленная на их количество) - (15+121-61+121+0+20)/6=36
мода ряда (число, которое в ряду встречается чаще других) - 121
размах ряда (разность наибольшего и наименьшего чисел) - 121-(-61)=182
1. Область определения: На ноль делить нельзя -->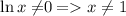 и х не отрицательный т.к. х под натуральным логарифмом. Итоге: x∈[0;1)∪(1;+∞)
и х не отрицательный т.к. х под натуральным логарифмом. Итоге: x∈[0;1)∪(1;+∞)
2. Функция общего вида т.к. f(-x)≠±f(x)
3. Точки пересечения с осями:
4. Исследование с 1ой производной:
см. внизу.
5. Исследование со 2ой производной:
см. внизу.
6. Асимптоты:
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: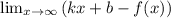
Находим коэффициент k: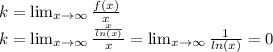
Находим коэффициент b: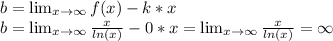
Предел равен ∞, следовательно, наклонные асимптоты функции отсутствуют.
Найдем вертикальные асимптоты. Для этого определим точки разрыва: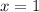
Находим переделы в точке 1: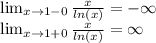
Значит точка разрыва II рода и является вертикальной асимптотой.