В равенстве слева сумма имеет общий член
1) Базис индукции:
2) Предположим, что и для верно равенство
3) Индукционный переход:
Равенство выполняется для всех натуральных n. Что и требовалось доказать.
В равенстве слева сумма имеет общий член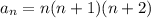
1) Базис индукции: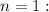
2) Предположим, что и для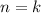
верно равенство
3) Индукционный переход:
Равенство выполняется для всех натуральных n. Что и требовалось доказать.