Вертикальные асимптоты: x = 2
Горизонтальные асимптоты: y = 3
Нет наклонных асимптот
Объяснение:
Выясним, при каких значениях переменной функция 3 x + 1 x − 2 не определена. x = 2
Рассмотрим рациональную функцию
, где n - степень числителя, а m - степень знаменателя.
1. Если n < m , то ось x, y = 0 , является горизонтальной асимптотой.
2. Если n = m , то горизонтальной асимптотой является прямая
Если n > m , то не существует горизонтальной асимптоты (только наклонная асимптота).
Найдем n и m
n = 1 ; m = 1
Поскольку n = m , горизонтальная асимптота является прямой , где a = 3 и b = 1
y = 3
Наклонных асимптот нет, поскольку степень числителя меньше либо равна степени знаменателя.
Это множество всех асимптот.
Как я поняла нужно решить 2 квадратных неравенства. Так?
Тогда решаем первое
х2-6х+9<=0
x2-6x+9=0
D=36-4*9=0, то есть корень 1
х=(6+0)/2=3
Значит графиком является парабола, пересекающая ось х в точке3, ветви вверх
Значит квадратный трехчлен нигде не будет <0, но так как нужно еще рассмотреть случай когда он=0, то решением будет точка 3
ответ: 3
2) -х2+12х-36>0 т.е.
(умножаем на -1) х2-12х+36=0
D=144-4*36=0, т.е одно решение
x=12/2=6 Квадратный трехчлен пересекает ось х в точке 6, ветви вниз
Т.е. нет точек когда он>0
ответ: Нет решения или решением является пустое множество
Вертикальные асимптоты: x = 2
Горизонтальные асимптоты: y = 3
Нет наклонных асимптот
Объяснение:
Выясним, при каких значениях переменной функция 3 x + 1 x − 2 не определена. x = 2
Рассмотрим рациональную функцию
1. Если n < m , то ось x, y = 0 , является горизонтальной асимптотой.
2. Если n = m , то горизонтальной асимптотой является прямая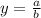
Если n > m , то не существует горизонтальной асимптоты (только наклонная асимптота).
Найдем n и m
n = 1 ; m = 1
Поскольку n = m , горизонтальная асимптота является прямой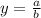
, где a = 3 и b = 1
y = 3
Наклонных асимптот нет, поскольку степень числителя меньше либо равна степени знаменателя.
Это множество всех асимптот.
Вертикальные асимптоты: x = 2
Горизонтальные асимптоты: y = 3
Нет наклонных асимптот
Как я поняла нужно решить 2 квадратных неравенства. Так?
Тогда решаем первое
х2-6х+9<=0
x2-6x+9=0
D=36-4*9=0, то есть корень 1
х=(6+0)/2=3
Значит графиком является парабола, пересекающая ось х в точке3, ветви вверх
Значит квадратный трехчлен нигде не будет <0, но так как нужно еще рассмотреть случай когда он=0, то решением будет точка 3
ответ: 3
2) -х2+12х-36>0 т.е.
(умножаем на -1) х2-12х+36=0
D=144-4*36=0, т.е одно решение
x=12/2=6 Квадратный трехчлен пересекает ось х в точке 6, ветви вниз
Т.е. нет точек когда он>0
ответ: Нет решения или решением является пустое множество