на рисунке 1.11 изображён график функции y=g( x) , определённой на промежутке ( -4, 4). пользуясь графиком, найдите наибольшее и наименьшее значение функции на промежутке: 1) ( -3;-2) 2) ( -3; -1) 3) ( -3;1)

Показать ответ

Ответ:

miras39

14.08.2022 03:40

Итак, ситуация номер 1 - имеется единственное решение:

Если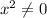 $x^2\neq 0$ , то имеется либо 2 и более корней, либо их вообще нет.

Мы знаем, что x=0, тогда

$-a^3-a=0\\a(a^2+1)=0\\a=0$

Решения для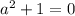 a^2+1=0 просто откидываем, комплексные числа нам неинтересны.

Первая ситуация разобрана, но проверку стоит провести:

$x^2=t\\t^2+t=0\\t=0$

Второе решение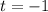 t=-1 не подходит, т.к.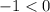

$t=0 \Rightarrow x^2=0 \Rightarrow x=0$

Проверка выполнена, имеется единственное решение при a=0

Вторая ситуация:

Необходимо 2 корня, значит значение t будет единственным!

$t^2+(a^2-a+1)t-a^3-a=0\\D=0 \\\therefore (a^2-a+1)^2-4(-a^3-a)=0\\a^4+a^2+1-2a^3+2a^2-2a+4a^3+4a=0\\a^4+2a^3+3a^2+2a+1=0$

Данное уравнение не имеет решений, и при любом значении a D>0 (D по t).

Т.е. мы не имеем решений для второй ситуации.

Третья ситуация:

Т.к. D>0, то и в третьей ситуации удовлетворяющих значений a просто нет.

0,0(0 оценок)

Ответ:

karavanov1

26.10.2020 19:44

первого раствора взяли 20 литров, а второго - 80 литров.

Объяснение:

Пусть 30%- го раствора взяли х л, а 55%- го раствора - у л, тогда по условию

х + у = 100.

Кислоты в первом растворе 0,3•х л, во втором растворе 0,55•у л, всего 0,3х + 0,55у. По условию в получившейся смеси 0,5•100 = 50 (л) кислоты, составим уравнение: 0,3х + 0,55у = 50.

Оба условия выполняются одновременно, составим и решим систему уравнений:

{х + у = 100,

{0,3х + 0,55у = 50;

{ у = 100 - х,

{0,3х + 0,55у = 50;

{ у = 100 - х,

{0,3х + 0,55•(100 - х) = 50;

{ у = 100 - х,

{0,3х + 55 - 0,55х = 50;

{ у = 100 - х,

{- 0,25х = 50 - 55;

{ у = 100 - х,