Поскольку, любое уравнение можно поделить на его старший коэффициент, то будем считать, для удобства, что мы рассматриваем два приведенных кубических уравнения с рациональными коэффициентами.
, - рациональные числа.
Поскольку, данные уравнения имеют общий корень, то уравнение, являющееся их разностью, тоже содержит этот корень:
, поскольку коэффициенты уравнений непропорциональны, то все коэффициенты полученного квадратного уравнения ненулевые.
А значит, данный общий иррациональный корень принимает вид : , где - рациональные числа, при этом не полный квадрат, отсюда в частности .
Попробуем показать, что если корень уравнения
, то и корень данного уравнения , и наоборот. Сделаем некоторое упрощение.
Если число является корнем данного уравнения , то сделаем замену: , тогда после раскрытия скобок данное уравнение так же будет с рациональными коэффициентами и будет иметь корень
Такое уравнение примет вид :
, - рациональные числа.
Учитывая, что
Предположим, что , но тогда , учитывая, что - не полный квадрат, то левая часть равенства иррациональна, а правая рациональна, что невозможно. То есть мы пришли к противоречию, а значит :
Таким образом:
Аналогично, доказывается, что если корень данного уравнения, то и корень этого уравнения.
Таким образом, мы доказали, что если корень уравнения
, то и корень данного уравнения и наоборот. Аналогично доказывается этот факт и для уравнения:
.
А значит, данные кубические многочлены имеют еще один общий иррациональный корень.
Поскольку, любое уравнение можно поделить на его старший коэффициент, то будем считать, для удобства, что мы рассматриваем два приведенных кубических уравнения с рациональными коэффициентами.
Поскольку, данные уравнения имеют общий корень, то уравнение, являющееся их разностью, тоже содержит этот корень:
А значит, данный общий иррациональный корень принимает вид :
, где 
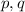- рациональные числа, при этом 
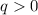не полный квадрат, отсюда в частности 
.
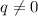Попробуем показать, что если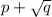
корень уравнения
Если число
является корнем данного уравнения , то сделаем замену: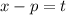 
, тогда после раскрытия скобок данное уравнение так же будет с рациональными коэффициентами и будет иметь корень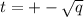 
Такое уравнение примет вид :
Учитывая, что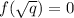
Предположим, что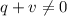
, но тогда , учитывая, что 
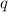- не полный квадрат, то левая часть равенства иррациональна, а правая рациональна, что невозможно. То есть мы пришли к противоречию, а значит :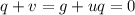 
Таким образом:
Аналогично, доказывается, что если![-\sqrt[]{q}](/tpl/images/1361/5367/ad7ea.png)
корень данного уравнения, то и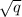 
корень этого уравнения.
Таким образом, мы доказали, что если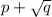
корень уравнения
А значит, данные кубические многочлены имеют еще один общий иррациональный корень.
Что и требовалось доказать.
1)
ОДЗ: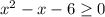
⇒ 
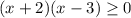⇒ ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
два корня
или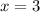 
C учетом![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
получаем ответ:
2)
ОДЗ: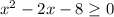
⇒ 
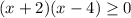⇒ ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
два корня
или 
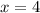
C учетом![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
получаем ответ:
3)
Так как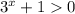
при любых х, возводим данное неравенство в квадрат:
D=16-12=4
Показательная функция с основанием 3 возрастает
О т в е т. (0;1)
4)
Так как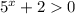
при любых х, возводим данное неравенство в квадрат:
D=36-20=16
Показательная функция с основанием 5 возрастает
О т в е т. (0;1)