ответ: Одночленом - называется произведение чисел, переменных и их натуральных степеней.
Каждое из чисел 1, 7, 1 002, 0, −1, −7, 0,8, 1/4, - это одночлен. Любая переменная, к примеру, a, b, p, q, t, x, y, z – это тоже одночлены по определению. Одночленами являются и степени чисел и переменных, например, 23, (−3,41)7, x2 и t115. Но наиболее яркими представителями одночленов являются произведения чисел, переменных и их степеней: 5·x, 7·(−3)·x·y3·6, x·x·y3·x·y2·z и т.п. Из приведенных примеров видно, что в составе одночлена может быть как одно, так и несколько чисел, как одна, так и несколько переменных и их степеней, причем они могут повторяться.
Многочленом называется сумма одночленов.
Одночлены, входящие в состав многочлена, называют его членами.
Членами многочлена 4xy – 3ab являются 4xy и – 3ab .
Если многочлен состоит из двух членов, то его называют двучленом:
5xy – 7ab ; y+5b; 7a+13a.
Если из трех – трехчленом:
5x y – 7a +5 ; y+5b– 3x ; 7a+13a+5ab .
Одночлен считают многочленом, состоящим из одного члена:
Вариант 2.
Задание 1.
1.
х = 18 :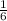
х = 18 * 6
х = 108
2.
7х + 11,9 = 0
7х = -11,9
х = -11,9 : 7
х = -1,7
3.
6х - 0,8 = 3х + 2,2
6х - 3х = 2,2 + 0,8
3х = 3
х = 3 : 3
х = 1
4.
5х - (7х + 7) = 9
5х - 7х - 7 = 9
-2х = 9 + 7
-2х = 16
х = 16 : (-2)
х = -8
Задание 2.
х км - на автобусе
9х км - на самолете
Составляем уравнение:
х + 9х = 600
10х = 600
х = 600 : 10
х = 60
60 км - на автобусе .
ответ: 60 км.
Задание 3.
Допустим на другом участке было х саженцев, тогда на первом - 5х .
После перевоза получилось:
х + 90 - другой участок.
5х - 50 - первый участок.
Составляем уравнение:
5х - 50 = х + 90
5х - х = 90 + 50
4х = 140
х = 140:4
х = 35
35 саженцев - на другом участке первоначально.
35 * 5 = 175 саженцев - было на первом участке первоначально.
ответ: 175, 35.
Задание 4.
6х - (2х - 5) = 2(2х + 4)
6х - 2х + 5 = 4х + 8
6х - 2х - 4х = 8 - 5
0х = 3
Нет решения.
ответ: Одночленом - называется произведение чисел, переменных и их натуральных степеней.
Каждое из чисел 1, 7, 1 002, 0, −1, −7, 0,8, 1/4, - это одночлен. Любая переменная, к примеру, a, b, p, q, t, x, y, z – это тоже одночлены по определению. Одночленами являются и степени чисел и переменных, например, 23, (−3,41)7, x2 и t115. Но наиболее яркими представителями одночленов являются произведения чисел, переменных и их степеней: 5·x, 7·(−3)·x·y3·6, x·x·y3·x·y2·z и т.п. Из приведенных примеров видно, что в составе одночлена может быть как одно, так и несколько чисел, как одна, так и несколько переменных и их степеней, причем они могут повторяться.
Многочленом называется сумма одночленов.
Одночлены, входящие в состав многочлена, называют его членами.
Членами многочлена 4xy – 3ab являются 4xy и – 3ab .
Если многочлен состоит из двух членов, то его называют двучленом:
5xy – 7ab ; y+5b; 7a+13a.
Если из трех – трехчленом:
5x y – 7a +5 ; y+5b– 3x ; 7a+13a+5ab .
Одночлен считают многочленом, состоящим из одного члена:
2x ; 3 ; 0 ; 7xy.