Войти Регистрация Спроси ai-bota

Наибольшее значение функции

Наибольшее значение функции

Показать ответ

Ответ:

ераврлга

19.10.2021 18:40

Объяснение:

Непрерывная функция f(x) достигает своего наибольшего значения либо на концах отрезка, либо в точках, где f'(x)=0.

f(x)=x*(3-2x)^2=x*(9-12x+4x^2)=9x-12x^2+4x^3

$f'(x)=9-24x+12x^2=12x^2-24x+9;\\f'(x)=0; 12x^2-24x+9=0;\\D=b^2-4ac=(-24)^2-4*12*9=576-432=144;\\x_1=\frac{-b+\sqrt{D}}{2a}=\frac{24+\sqrt{144}}{24}=\frac{24+12}{24}=\frac{36}{24}=1,5$

$x_2=\frac{-b-\sqrt{D}}{2a}=\frac{24-\sqrt{144}}{24}=\frac{24-12}{24}=\frac{12}{24}=0,5$

x_1=1,5 не принадлежит отрезку [0; 1].

Вычислим значение f(x) на концах отрезка и в точке x=0,5.

f(0) = 0;

f(1) = 1;

f(0,5) = 0,5*(3-2*0.5)² = 0.5*2²=0.5*4=2.

Наибольшее значение f(x) равно 2.

0,0(0 оценок)

Ответ:

shevyakova2018

19.10.2021 18:40

$\boxed{max: f(0,5) = 2}$

Объяснение:

$f(x) = x(3 - 2x)^{2} ; x\in [0;1]$

$f(x) = x(3 - 2x)^{2} = x(9 - 12x + 4x^{2} ) = 4x^{3} - 12x^{2} + 9x$

$f'(x) = (4x^{3} - 12x^{2} + 9x)' = (4x^{3})' - (12x^{2})' + (9x)' = 4(x^{3})' - 12(x^{2})' + 9(x)'=$

$= 12x^{2} - 24x + 9$

f'(x) = 0

$12x^{2} - 24x + 9 = 0|:3$

$4x^{2} - 8x + 3 = 0$

$D = 64 - 4 * 4 * 3 = 64 - 48 = 16 = 4^{2}$

$x_{1} = \dfrac{8 + 4}{2 \cdot 4} = \dfrac{12}{8} = 1,5$

$x_{1} = \dfrac{8 - 4}{2 \cdot 4} = \dfrac{4}{8} = 0,5$

При $x \in \mathbb R$

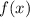Функция f(x) убывает при $x \in [0,5;1,5]$

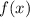Функция f(x) возрастает при $x \in (-\infty;0,5] \cup [1,5;+\infty)$

При $x\in [0;1]$

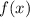Функция f(x) убывает при $x \in [0,5;1]$

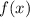Функция f(x) возрастает при $x \in [0;0,5]$

$f(0) = 4 * 0^{2} - 12 * 0^{2} + 9 * 0 = 0$

$f(1) = 4 * 1^{3} - 12 * 1^{2} + 9 * 1 = 4 - 12 + 9 = 1$

$max: f(0,5) = 4 * 0,5^{3} - 12 * 0,5^{2} + 9 * 0,5 = 0,5 - 3 + 4,5 = 2$

min: f(0) = 0

Наибольшее значение функции

Наибольшее значение функции

Наибольшее значение функции

0,0(0 оценок)

Популярные вопросы: Алгебра

LEVATOR

10.07.2021 05:06

Докажите, что при любом натуральном n: а) если n^2-1 четно, то n^2-1 делится на 8; б) если n^3-4n четно, то n^3-4n делится на 48...

daniilkornev05

10.07.2021 05:06

Log12 корень из 14 · log14 корень из12...

Solncelunatik

10.07.2021 05:06

Сколько последовательных натуральных чисел, начиная с 1, нужно сложить, чтобы их сумма была равна 105...

narenkovaa

10.07.2021 05:06

Найдите значение выражения log2 a1/3 если log4 a3=9...

Vita1968

10.07.2021 05:06

Верно ли утверждение? используя каждую из цифр 1 1 2 и 3 по одному разу , можно составить ровно 24 различных четырехзначных чисел.....

крут6776

10.07.2021 05:06

Іть розв’язати cистему рівнянь xy=60; x2+y2=169...

ritagribaleva

10.07.2021 05:06

956^2-44^2/406 + 38^2-17^2/72^2-12^2...

cghjy6655

12.04.2021 10:38

Найдите значение выражения 3/на корень из 2*sin 2а , если известно: sin а=-корень из 3/3; а принадлежит отезку от (п; 3п/2) вообще на кдр ничего не решил есть шанс...

vasvas12

12.04.2021 10:38

Решить в целых числах уравнение: mn = m + n + 1. ответ представить в виде суммы всех целых решений (m, n) данного уравнения....

berezinaanna199

17.11.2020 03:42

Разложите многочлен на множители (2a-b)^3-(2a+b)^3...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку