Чтобы найти область значения функции, надо сначала найти ординату вершины параболы(n), а для того чтобы найти ординату вершины параболы, надо сначала найти абсциссу вершины параболы по формуле m=- затем подставить вместо х значение m, а потом уже найти n:
m=- =- = - = -4
< br/ > n = f(m) =-8*(-4)+1 = -16+32+1=17
Мы нашли ординату вершины параболы. Это её наибольшее значение. Поэтому все остальные значения параболы будут либо меньше, либо равны 17(≤17).
Поэтому ответ таков: Е(у)=(-∞;17]. Если что, Е(у)- это область значения.
11 в любой степени кончается на 1. 19 в нечетной степени кончается на 9.
Их сумма кончается на 1+9=10, то есть на 0, а значит, делится на 5.
Осталось доказать, что это число делится на 3.
11=3*3+2; 11^2019 = (3*3+2)^2019 = 2^2019.
Здесь и дальше знак = означает "такой же остаток при делении на 3".
2^2019 = (2^3)^673 = 8^673 = 2^673 = 2^3*2^670 = 8*(2^10)^67 = 2*1024^67 =
= 2*(3*341+1)^67 = 2*1^67 = 2
Таким образом, 11^2019 имеет при делении на 3 остаток 2.
19 = 3*6+1; 19^2019 = (3*6+1)^2019 = 1^2019 = 1.
Таким образом, 19^2019 имеет при делении на 3 остаток 1.
Сумма этих чисел имеет остаток 2+1=3, то есть делится нацело.
Что и требовалось доказать.
Чтобы найти область значения функции, надо сначала найти ординату вершины параболы(n), а для того чтобы найти ординату вершины параболы, надо сначала найти абсциссу вершины параболы по формуле m=-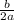
затем подставить вместо х значение m, а потом уже найти n:
m=-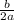
=-
= -
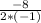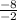= -4
< br/ > n = f(m) =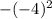
-8*(-4)+1 = -16+32+1=17
Мы нашли ординату вершины параболы. Это её наибольшее значение. Поэтому все остальные значения параболы будут либо меньше, либо равны 17(≤17).
Поэтому ответ таков: Е(у)=(-∞;17]. Если что, Е(у)- это область значения.
УДАЧИ ВАМ ВО ВСЁМ)))!