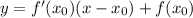logo
Войти Регистрация Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
lckzgizigzly
lckzgizigzly
18.04.2023 11:14 •  Алгебра

Напишите уравнение касательнойк графику f(x)=cos^2×6x в точке x0= пи/24

Показать ответ
Ответ:
mischkulentsov
mischkulentsov
10.10.2020 18:49

Уравнение касательной к графику: y = f'(x_{0} )(x - x_{0} ) +f(x_{0} )

f'(x) = cos^{2}6x  - сложная функция: косинус -  внешняя функция, а 6x - внутренняя.

f'(x) = 2*cos^{2-1} (6x) * (cos(6x)'*(6x)' = 2*cos(6x)*( -sin(6x))*6 = -12*cos(6x)*sin(6x) = -6*sin(12x);\\

f'(x_{0} ) = -6 *sin (12\pi /24) = -6*sin(\pi /2) = -6;\\f(x_{0} ) = cos^{2}(6\pi /24) = cos^{2}(\pi /4) = \frac{1}{2} ;\\y = -6*(x - \pi /24) + \frac{1}{2}

0,0(0 оценок)
Популярные вопросы: Алгебра
Sasha2771
Sasha2771
30.04.2022 14:11
В течении суток,начиная с 0 часов,каждый час измерялась температура воздуха:11;11;9;8;10;11;11;12;12;14;15;16;16;17;18;17;15;15;14;12;11;11;10;10. Для полученного ряда...
Jkbts
Jkbts
10.05.2021 22:40
сделать Дз к завтрашнему дню я уже сам не справляюсь​...
Abdueva
Abdueva
19.02.2022 05:13
3 Перемножь: (−2−a)(b+1) . −2−2b−ab−a −2b+ab+a−2 +2b+ab+a+2 +2b−ab−a+2 4...
kri2221
kri2221
02.03.2022 18:22
Знайти вертикальні кути, якщо 2 x сума 62°...
gamer0072
gamer0072
02.03.2022 18:22
1)c¹¹:c⁶ 2)c⁶*c⁵:c¹⁰= решить это степени свойства 7класс алгебра...
ellalavrina
ellalavrina
24.07.2021 12:26
В течении суток,начиная с 0 часов,каждый час измерялась температура воздуха:11;11;9;8;10;11;11;12;12;14;15;16;16;17;18;17;15;15;14;12;11;11;10;10. Для полученного ряда...
sd16sv
sd16sv
25.12.2020 08:58
И! сформулиравать алгоритм умножения многочлен на одночлен...
IvanPAW2145778
IvanPAW2145778
25.12.2020 08:58
Вычислите ctg 585° -2*cos 1440°+√2*sin1125°...
lianagabrielya
lianagabrielya
12.12.2020 21:09
Составьте квадратное уравнение по его корням 1 и 2...
Diana451111
Diana451111
12.12.2020 21:09
Розкладіть на множники : 3а-3в+ах -вх...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку
О НАС
СООБЩЕСТВО
ПОМОЩЬ
App
.
.
logo
Начни делиться знаниями
Вход Регистрация
Что ты хочешь узнать?
Спроси ai-бота