График - парабола с вершиной в точке (5;1) , ветви вверх, ось симметрии х=5 . Получена из параболы путём растяжения вдоль оси ОУ в 2 раза, затем она смещена вдоль оси ОХ вправо на 5 единиц и вдоль оси ОУ вверх на 1 единицу .
Пересечение с осью ОХ нет ⇒ при .
Пресечение с осью ОУ в точке .
Убывает при , возрастает при .
Точка минимума минимальное значение функции .
График - парабола, с вершиной в точке (2;-3) , ветви вверх, ось симметрии х= -2 . Получена при перемещении графика вдоль оси ОХ влево на 2 единицы и вдоль оси ОУ вниз на 3 единицы .
Решение: 1) пусть х кг - вес третьего слитка, у кг - вес меди в третьем слитке. по условию в 1-ом слитке 30% меди, тогда 5·0,3 = 1,5 (кг) - чистой меди в первом слитке. по условию во 2-ом слитке тоже 30% меди, тогда 3·0,3 = 0,9 (кг) - чистой меди во втором слитке. 2) если первый слиток сплавили с третьим, то вес получившегося слитка равен (5 + х) кг, а количество в нём меди - (1,5 + у) кг. по условию содержание меди при этом получилось равным 56%. составим уравнение:3) если второй слиток сплавить с третьим, то вес получившегося слитка равен (3 + х) кг, а количество в нём меди - (0,9 + у) кг. по условию содержание меди при этом получилось равным 60%. составим уравнение:4) составим и решим систему уравнений:сложив почленно обе части уравнения, получим, что 10 кг - вес третьего слитка6,9 кг меди в третьем слитке 5) найдём процентное содержание меди в третьем слитке: % меди в третьем слитке. ответ: 69 %.
График - парабола с вершиной в точке (5;1) , ветви вверх, ось симметрии х=5 . Получена из параболы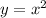 путём растяжения вдоль оси ОУ в 2 раза, затем она смещена вдоль оси ОХ вправо на 5 единиц и вдоль оси ОУ вверх на 1 единицу .
путём растяжения вдоль оси ОУ в 2 раза, затем она смещена вдоль оси ОХ вправо на 5 единиц и вдоль оси ОУ вверх на 1 единицу .
Пересечение с осью ОХ нет ⇒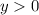 при
при 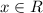 .
.
Пресечение с осью ОУ в точке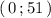 .
.
Убывает при![x\in (-\infty ;\, 5\ ]](/tpl/images/1657/0857/c774b.png) , возрастает при
, возрастает при 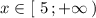 .
.
Точка минимума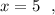 минимальное значение функции
минимальное значение функции 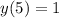 .
.
График - парабола, с вершиной в точке (2;-3) , ветви вверх, ось симметрии х= -2 . Получена при перемещении графика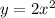 вдоль оси ОХ влево на 2 единицы и вдоль оси ОУ вниз на 3 единицы .
вдоль оси ОХ влево на 2 единицы и вдоль оси ОУ вниз на 3 единицы .