Найдите координаты вершины параболы.
f(x)=x^2-5x+6

6.   -5 ≤ А ≤ 35

ответ 4).

7.  

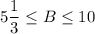
ответ 1)

Объяснение:

Требуется оценить выражение.

6.

-4 ≤ a ≤ 1;     A = 3 - 8a

Если обе части неравенства умножить или разделить на отрицательное число, знак неравенства перевернется.

Умножим все части неравенства на (-8), перевернув знаки неравенства:

-4 ≤ a ≤ 1     | · (-8)

32 ≥ -8a ≥ -8

или

-8 ≤ -8а ≤ 32

Если ко всем частям неравенства прибавить или отнять одно и то же число, то получим неравенство, равносильное данному.

Прибавим ко всем частям неравенства 3:

3 - 8 ≤ 3 - 8а ≤ 3 + 32

-5 ≤ 3 - 8а ≤ 35

-5 ≤ А ≤ 35

ответ 4).

7.

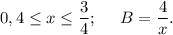
Если a и b - положительные числа и а > b, то 1/а < 1/b.

Переведем 0,4 в обыкновенную дробь.

Перевернем наши дроби, при этом знак неравенства тоже перевернется:

Умножим все части неравенства на 4:

ответ 1)

да

Объяснение:

Пусть числитель равен х, тогда знаменатель (х +1). Исходная дробь будет выглядеть как х / (х + 1). Измененная дробь — х / (х + 3).

Разность дробей составляет 1/4. Получаем уравнение:

х / (х + 1) - х / (х + 3) = 1 / 4;

4 * х * (х + 3) - 4 * х * (х + 1) = (х +1) * (х + 3);

4 * х² + 12 * x - 4 * x² - 4 x = x² + 4 * x + 3;

x² - 4 * x +3 = 0;

D = 16 - 4 * 1 * 3 = 16 - 12 = 4;

х1 = (4 - 2) / 2 = 1;

х2 = (4 + 2) / 2 = 3.

Задача имеет два решения:

1) х1 = 1;  y1 = x1 + 1 = 2.

Первая дробь, удовлетворяющая условиям — 1/2.

Проверка:

1/2 - 1/4 = 1/4.

2) х2 = 3; y2 = x2 + 1 = 4.

Вторая дробь, удовлетворяющая условиям — 3/4.

Проверка:

3/4 - 3/6 = 1/4.