Производительность первой бригады составляет 3 единицы в день.
Производительность второй бригады составляет 9 единицы в день.
К концу 4- го дня, объем работы выполненный первой бригадой оценивается в 12 единиц, а второй в 36 единиц. Разница составила 24 единицы.
Начиная с пятого дня, производительность первой бригады составляет уже 10 единиц в день, а второй 2 единицы в день.
С этого момента представим график, где оси X соответствует количество дней, а оси Y объем выполненной работы, начиная с пятого дня. График первой бригады начинается в точке (0;0) и каждое последующее значение у больше значения x в 10 раз. График второй бригады начинается в точке (0;24) и каждое последующее значение у больше значения x в 2 раза.
В виде системы линейных уравнений это будет выглядеть следующим образом:
y=2x+24
y=10x
10x=2x+24
8x=24
x=3
То есть через три дня обе бригады одновременно достигнут равного объема выполненной работы.
Данная функция - квадратичная (функция, уравнение которой включает в себя переменную ). Стандартный вид функции: .
То есть в нашей функции это , это и это .
Стандартный вид функции: .2. Определим направление параболы.
График квадратичной функции - парабола (геометрическое место точек, равноудалённых от данной прямой). Ветви параболы могут быть направлены вверх и вниз.
Если коэффициент при переменной положительный, то ветви параболы направлены вверх. Если же коэффициент отрицательный, то ветви параболы направлены вниз.
. Здесь , поэтому ветви параболы направлены вниз.3. Вычислим координату вершины параболы.
Координата вершины параболы - значение . Если квадратичная функция записана в стандартном виде , воспользуемся коэффициентами и :
В функции коэффициенты . Т.е. координата вершины параболы: .4. Найдём соответствующее значение .
Мы ищем максимум функции, так как ветви параболы направлены вниз. Чтобы найти максимум нужно подставить в исходную функцию найденное значение .
На выполнение заказа потребовалось 7 дней
Объяснение:
Производительность первой бригады составляет 3 единицы в день.
Производительность второй бригады составляет 9 единицы в день.
К концу 4- го дня, объем работы выполненный первой бригадой оценивается в 12 единиц, а второй в 36 единиц. Разница составила 24 единицы.
Начиная с пятого дня, производительность первой бригады составляет уже 10 единиц в день, а второй 2 единицы в день.
С этого момента представим график, где оси X соответствует количество дней, а оси Y объем выполненной работы, начиная с пятого дня. График первой бригады начинается в точке (0;0) и каждое последующее значение у больше значения x в 10 раз. График второй бригады начинается в точке (0;24) и каждое последующее значение у больше значения x в 2 раза.
В виде системы линейных уравнений это будет выглядеть следующим образом:
y=2x+24
y=10x
10x=2x+24
8x=24
x=3
То есть через три дня обе бригады одновременно достигнут равного объема выполненной работы.
Итого: 4+3=7 дней.
Данная функция - квадратичная (функция, уравнение которой включает в себя переменную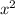 ). Стандартный вид функции:
). Стандартный вид функции: 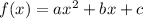 .
.
То есть в нашей функции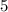 это
это  ,
, 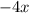 это
это 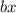 и
и 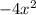 это
это 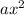 .
.
Стандартный вид функции:График квадратичной функции - парабола (геометрическое место точек, равноудалённых от данной прямой). Ветви параболы могут быть направлены вверх и вниз.
Если коэффициент при переменной
при переменной 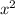 положительный, то ветви параболы направлены вверх. Если же коэффициент отрицательный, то ветви параболы направлены вниз.
положительный, то ветви параболы направлены вверх. Если же коэффициент отрицательный, то ветви параболы направлены вниз.
Координата вершины параболы - значение
вершины параболы - значение 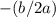 . Если квадратичная функция записана в стандартном виде
. Если квадратичная функция записана в стандартном виде 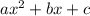 , воспользуемся коэффициентами
, воспользуемся коэффициентами  и
и 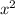 :
:
В функцииМы ищем максимум функции, так как ветви параболы направлены вниз. Чтобы найти максимум нужно подставить в исходную функцию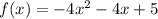 найденное значение
найденное значение  .
.
Точка максимума функции равна .
.