При :
Так как , то k . Теперь подставляем каждое из этих значений в корень нашего уравнения.
При получаем .
ответ: ; .
При![x \in [-\frac{3\pi}{2}; 2\pi]](/tpl/images/1557/8858/a63b2.png) :
:
Так как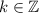 , то k
, то k 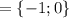 . Теперь подставляем каждое из этих значений в корень нашего уравнения.
. Теперь подставляем каждое из этих значений в корень нашего уравнения.
При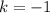 получаем
получаем 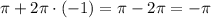 .
.
При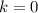 получаем
получаем 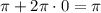 .
.
ответ: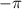 ;
; 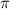 .
.