Все в объяснениях.
Объяснение:
1. Постройте график функции y=f(x).
Гипербола, полученная сдвигом графика у= на 1 вверх по оу. у(-2)=0,5 ;у(-1)=1 ;у(-2)=0,5 ;у(2)=-0,5 ;у(1)=-1 ;у(2)=-0,5
2. f '(x)= ( ) ' = .
3. Уравнения касательной y =к (x −x₀)+f (x₀) .
Прямая y= , к=1\4.
Найдем точку касания
(x-2)²=0 , x=2.
f (2)=-1\2+1=0,5
y =0,25* (x −2)+0,5
у=0,25х
Вторая касательная пройдет через х=-2
f (-2)=1\2+1=1,5
y =0,25* (x −2)+1,5
у=0,25х+1
4. Наименьшее значение функции у'=(x−f(x) ) '=(х)' =
=1 -= .
у'=0 , ,х=1 , х=-1.
На промежутке [1/2;∞) лежит только х=1
у'______[1\2] - - - - -(1)+ + + + +
y ↓ ↑
x=1 точка минимума.
Наименьшее значение может быть при х=1\2 или х=1:
у(1\2) = .
у(1)= 1+1-1=1.
Наименьшее значение функции х-f(x) равно -0,5
y-2x<-4
y<2x-4
y=2x-4 - линейная функция, график прямая
х | 0 | 2
у | -4 | 0
неравенство строгое, => прямая пунктирная(не включена, точки прямой не являются решением неравенства)
прямая делит координатную плоскость на две полуплоскости.
выберем произвольную точку А(1;1), координаты точки А подставим в неравенство:
1<2×1-4
1<-2 ложно,
=> точка А(1;1) и все точки лежащие с ней в одной полуплоскости не являются решением неравенства.
смотри вложение(решение - штриховка красным цветом
Все в объяснениях.
Объяснение:
1. Постройте график функции y=f(x).
Гипербола, полученная сдвигом графика у=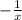
на 1 вверх по оу. у(-2)=0,5 ;у(-1)=1 ;у(-2)=0,5 ;у(2)=-0,5 ;у(1)=-1 ;у(2)=-0,5
2. f '(x)= (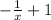
) ' =
.
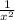3. Уравнения касательной y =к (x −x₀)+f (x₀) .
Прямая y=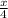
, к=1\4.
Найдем точку касания
(x-2)²=0 , x=2.
f (2)=-1\2+1=0,5
y =0,25* (x −2)+0,5
у=0,25х
Вторая касательная пройдет через х=-2
f (-2)=1\2+1=1,5
y =0,25* (x −2)+1,5
у=0,25х+1
4. Наименьшее значение функции у'=(x−f(x) ) '=(х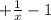
)' =
=1 -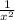
=
.
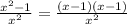у'=0 ,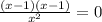
,х=1 , х=-1.
На промежутке [1/2;∞) лежит только х=1
у'______[1\2] - - - - -(1)+ + + + +
y ↓ ↑
x=1 точка минимума.
Наименьшее значение может быть при х=1\2 или х=1:
у(1\2) =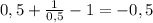
.
у(1)= 1+1-1=1.
Наименьшее значение функции х-f(x) равно -0,5
Объяснение:
y-2x<-4
y<2x-4
y=2x-4 - линейная функция, график прямая
х | 0 | 2
у | -4 | 0
неравенство строгое, => прямая пунктирная(не включена, точки прямой не являются решением неравенства)
прямая делит координатную плоскость на две полуплоскости.
выберем произвольную точку А(1;1), координаты точки А подставим в неравенство:
1<2×1-4
1<-2 ложно,
=> точка А(1;1) и все точки лежащие с ней в одной полуплоскости не являются решением неравенства.
смотри вложение(решение - штриховка красным цветом