Объяснение:
Посчитаем:
Тут выражение, равное разности степеней чисел 21 , 3 и 4
Свойство степени числа такое:
1. если показатель (цифра сверху) положительное (больше нуля), то пишем обычную степень .
2. если показатель равен нулю
3. если показатель меньше нуля, то пишем так:
Рассмотрим на нашем примере и посчитаем:
1) 21 в 0 степени - 1 по второму свойству.
2) 3 в степени -2 равно по 3 свойству.
3) 4 в степени -2 равно по 3 свойству.
А затем выполним над ними операции, приведя к общему знаменателю:
144, так как 144 делится и на 16, и на 9 , чтобы было удобнее считать.
- положительное число, то есть число. которое больше 0. Что и требовалось доказать.
представим 3^4=t =>t=x^logx(t) =>x^(log3(x))=x^logx(t) =>log3(x)=logx(t)
log3(x)=1/logt(x)=>log3(x)*logt(x)=1 => log3(x)*log3^4(x)=1 1/4(log3(x))^2=1
( log3(x))^2=4 log3(x)=+-2 x1=9 x2=1/9 одз х>0
2) log3(x)*log4(x)=4log4(3) log4(x^log3(x))=log4(3^4) x^log3(x)=3^4 x^log3(x)=x^(logx(3^4) log3(x)=logx(3^4) log3(x)=4logx(3) log3(x)=4/log3(x)
(log3(x)^2=4 log3(x)=+-2 log3(x)=-2 x1=3^-2=1/9 x2=3^2=9
Объяснение:
Посчитаем:
Тут выражение, равное разности степеней чисел 21 , 3 и 4
Свойство степени числа такое:
1. если показатель (цифра сверху) положительное (больше нуля), то пишем обычную степень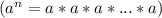 .
.
2. если показатель равен нулю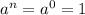
3. если показатель меньше нуля, то пишем так: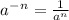
Рассмотрим на нашем примере и посчитаем:
1) 21 в 0 степени - 1 по второму свойству.
2) 3 в степени -2 равно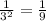 по 3 свойству.
по 3 свойству.
3) 4 в степени -2 равно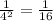 по 3 свойству.
по 3 свойству.
А затем выполним над ними операции, приведя к общему знаменателю:
144, так как 144 делится и на 16, и на 9 , чтобы было удобнее считать.
- положительное число, то есть число. которое больше 0. Что и требовалось доказать.