y наиб = 243
Объяснение:
Дана функция
Производная функции
y' = 0
ln3 > 0
2x - 6 = 0
x = 3
При х < 3 y' < 0, следовательно, функция у↓ (убывает)
При х > 3 y' > 0, следовательно, функция у↑ (возрастает)
Это значит, что х = 3 - точка минимума
y наиб = 243
Объяснение:
Дана функция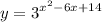
Производная функции
y' = 0
ln3 > 0
2x - 6 = 0
x = 3
При х < 3 y' < 0, следовательно, функция у↓ (убывает)
При х > 3 y' > 0, следовательно, функция у↑ (возрастает)
Это значит, что х = 3 - точка минимума