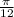------------------------------------------------------------------
Подстовляем значения у в уравнения.
при n=-1 уже начинаються отрицательные значения. Значит наименьшее положительное
------------------------------------------------------------------
Подстовляем значения у в уравнения.
при n=-1 уже начинаються отрицательные значения. Значит наименьшее положительное