Тождественное, т.е. тоже самое, схожее. Если убрать минус снизу у -5b-6y и поставить его перед числителем (см картинку мою), то получится -2x+a/6b+6y.
Знак "-" перед дробью можно внести либо в числитель, либо в знаменатель, но не туда и туда (иначе это будет уже 2 знака минус, т. е. в итоге - плюс) .
Мы вынесли минус в знаменателе и сделали его перед дробью, а потом внесли в числитель, в знаменателе естественно поменялись знаки, раз минус вынесли и в числители тоже, т.к. туда минус внесли.
Вариант 3.
Объяснение:
Тождественное, т.е. тоже самое, схожее. Если убрать минус снизу у -5b-6y и поставить его перед числителем (см картинку мою), то получится -2x+a/6b+6y.
Знак "-" перед дробью можно внести либо в числитель, либо в знаменатель, но не туда и туда (иначе это будет уже 2 знака минус, т. е. в итоге - плюс) .
Мы вынесли минус в знаменателе и сделали его перед дробью, а потом внесли в числитель, в знаменателе естественно поменялись знаки, раз минус вынесли и в числители тоже, т.к. туда минус внесли.
≈ 24,6°
Объяснение:
Для начала найдем вектор по координатам точек:
AB = {Bx - Ax; By - Ay; Bz - Az}
AB = {3 - 3; -2 - (-1); 2 - (-3)}
AB = {0; -1; 5}
CD = {Dx - Cx; Dy - Cy; Dz - Cz}
CD = {1 - 2; 2 - (-2); 2 - 3}
CD = {-1; 4; -1}
Теперь найдем скалярное произведение векторов:
AB · CD = ABx · CDx + ABy · CDy + ABz · CDz
AB · CD = 0 · (-1) + (-1) · 4 + 5 · (-1)
AB · CD = 0 - 4 - 5
AB · CD = -9
Затем найдем длины векторов:
|AB| =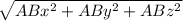
|AB| =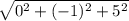
|AB| =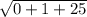
|AB| =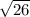
|CD| =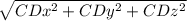
|CD| =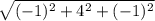
|CD| =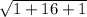
|CD| =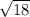
|CD| = 3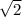
Найдем косинус угла между векторами:
cos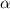
= 
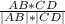
cos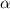
= 
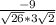
cos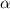
= 
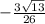
cos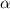
= ≈ -0.41602514716892186
И наконец-то находим по таблице брадисса угол, с найденого косинуса
Это ≈ 24,6°