Найдите положительный корень уравнения​

Пусть х ч - время работы одного крана, тогда (х + 5) ч - время работы другого крана.

Работу по разгрузке примем за единицу, тогда 1/х - работа, которую выполнит первый кран за 1 ч, 1/(х+5) - работа, которую выполнит второй кран за 1 ч, 1/6 - совместная работа за 1 ч. Уравнение:

1/х + 1/(х+5) = 1/6

Приводим обе части уравнения к общему знаменателю х · (х +5) · 6

(х + 5) · 6 + х · 6 = х · (х + 5)

6х + 30 + 6х = х² + 5х

х² + 5х - 12х - 30 = 0

х² - 7х - 30 = 0

D = b² - 4ac = (-7)² - 4 · 1 · (-30) = 49 + 120 = 169

√D = √169 = ±13

х = (-b±√D)/2a

х₁ = (7-13)/(2·1) = (-6)/2 = -3 (не подходит, так как < 0)

х₂ = (7+13)/(2·1) = 20/2 = 10 (ч) - время работы одного крана

10 + 5 = 15 (ч) - время работы другого крана

ответ: 10 ч и 15 ч.

 - красные

  - жёлтые

  - все шары

   все шары без одного, т.е. все оставшиеся.

По условию:      .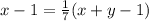

Получаем первое уравнение:

Ещё по условию:   .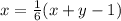

Второе уравнение:    

Левые части обоих уравнений равны, значит, их правые части равны между собой.

                     красныx шаров в коробке.

Подставим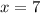    в уравнение  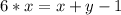   и получим:

                      жёлтыx шаров в коробке.

         всего шаров в коробке.

ответ:     7  красныx;

               36  жёлтых;

                43 всего шаров в коробке.