Объяснение:
°- вместо штриха
1) 2*2x=4x (табличные производные)
2) 3*4 (табличные производные)
3) По правилу нахождения производной от умножения
(х³+6х−3)° * (x+1) + (х³+6х−3) * (x+1)°= (3 +6) * (x+1) + (х³+6х−3)* 1=
3 +3 +6x +6 + х³+6х−3 =4 +3 +12x +3
4) По правилу нахождения производной от деления
(4х-7)° * (х²+4) -(4х-7)* (х²+4)° / (х²+4)^2 =
4(х²+4)- 2x(4х-7) / (х²+4)^2 =
4х²+16 -8х² -14x / (х²+4)^2 =
-4х² -14x +16 / (х²+4)^2
Объяснение:
°- вместо штриха
1) 2*2x=4x (табличные производные)
2) 3*4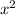 (табличные производные)
(табличные производные)
3) По правилу нахождения производной от умножения
(х³+6х−3)° * (x+1) + (х³+6х−3) * (x+1)°= (3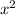 +6) * (x+1) + (х³+6х−3)* 1=
+6) * (x+1) + (х³+6х−3)* 1=
3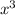 +3
+3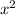 +6x +6 + х³+6х−3 =4
+6x +6 + х³+6х−3 =4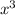 +3
+3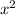 +12x +3
+12x +3
4) По правилу нахождения производной от деления
(4х-7)° * (х²+4) -(4х-7)* (х²+4)° / (х²+4)^2 =
4(х²+4)- 2x(4х-7) / (х²+4)^2 =
4х²+16 -8х² -14x / (х²+4)^2 =
-4х² -14x +16 / (х²+4)^2