Рисунок смотрите в приложении (на нем изображены равные векторы).
Векторы равны, когда они имеют равные длины и одинаковое направление (и при этом лежат на параллельных прямых или на одной и той же прямой).
а). Векторы и равны по модулю (то есть, равны их длины), как стороны квадрата, но имеют разное направление. Как видно из рисунка, угол между ними равен градусов (получаем, что это коллинеарные, но не равные векторы).
.
б). Векторы и равны по длине, лежат на параллельных прямых и имеют одинаковое направление. Значит, они равны.
.
в). Векторы и опять же имеют одинаковые длины. Но они никак не лежат на параллельных прямых, они являются перпендикулярными (так как угол квадрата - градусов).
Всё решается просто. так как cos2x=2*(cosx)^2-1 (эту формулу можно найти в учебнике или доказать) , то подставляя в уравнение получим: cos2x+4cosx-5=0 2*(cosx)^2-1+4cosx-5=0 (cosx)^2+2(cosx)-3=0 это простое квадратное уравнение относительно cosx. то есть получается два решения: cosx=1 и cosx=-3 но подходит только одно решение cosx=1, так как |cosx|< =1 осталось решить простое тригонометрическое уравнение cosx=1, по формуле тригонометрии cosx=a, x=(+/-)arccosa+2*pi*n pi-это знаменитое число 3,14159 n-любое целое число вот и всё решение.
Рисунок смотрите в приложении (на нем изображены равные векторы).
Векторы равны, когда они имеют равные длины и одинаковое направление (и при этом лежат на параллельных прямых или на одной и той же прямой).а). Векторы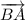 и
и 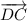 равны по модулю (то есть, равны их длины), как стороны квадрата, но имеют разное направление. Как видно из рисунка, угол между ними равен
равны по модулю (то есть, равны их длины), как стороны квадрата, но имеют разное направление. Как видно из рисунка, угол между ними равен 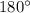 градусов (получаем, что это коллинеарные, но не равные векторы).
градусов (получаем, что это коллинеарные, но не равные векторы).
б). Векторы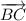 и
и 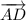 равны по длине, лежат на параллельных прямых и имеют одинаковое направление. Значит, они равны.
равны по длине, лежат на параллельных прямых и имеют одинаковое направление. Значит, они равны.
в). Векторы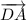 и
и 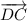 опять же имеют одинаковые длины. Но они никак не лежат на параллельных прямых, они являются перпендикулярными (так как угол квадрата -
опять же имеют одинаковые длины. Но они никак не лежат на параллельных прямых, они являются перпендикулярными (так как угол квадрата - 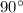 градусов).
градусов).
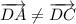
ответ:а) нет;
б) да;
в) нет.