x^2-6x+5=0. решим эти уравнения любым удобным , для меня это теорема обратная Т.Виета
произведение корней равно минус 10, а сумма равна 3, очевидно это 5 и минус 2, произведение корней равно 5, а сумма 6, очевидно это 5 и 1, и очень хорошо, что есть одинаковые корни. Мы имеем право записать квадратный трехчлен как a(x-x1)*(x-x2), где х1 и х2 это корни квадратного трехчлена, a - коэффициент перед старшей степенью. Тогда на х-5 можно сократить, окончательно получим.
1 вариант
№1
а) (a-5)²=a²-10a+25 б) (6a+b)²=36a²+12ab+b²
в) (4a-1)(4a+1)=16a²-1 в) (a+2b)³=a³+6a²b+6ab²+8b³
№2
(a-6)²-(36+5a)=a²-12a+36-36-5a=a²-17a
№3
а) 3x²+9xy=3x(x+3y) б) 10x⁵-5x=5x(2x⁴-1)
№4
а) (a+3)-2(a+3)=(a+3)(1-2)=-1(a+3) б) ax-ay+5x-5y=a(x-y)+5(x-y)=(x-y)(a+5)
в) a²+4ab+4b²=(a+2b)²=(a+2b)(a+2b)
№5
а) (y²-2a)(2a+y²)=y⁴-4a²
б) (3x²+x)²=9x⁴+6x³+x²
№6
а) 4x²y²-9a⁴=(2xy+3a²)(2xy-3a²) б) 25a²-(a+3)²=(5a-a-3)(5a+a+3)=(4a-3)(6a+3)
в) 27m³+n³=(3m+n)(9m²-3mn+n²)
№7
а) 9y²-25=0
9y²=25
y²=25/9
y₁,₂=±5/3=±1 2/3
б) (x+2)(x-2)-(x-3)²=-1
x²-4-x²+6x-9=-1
6x=12
x=2
№8
а) 35²-25²=(35-25)(35+25)=10*60=600
б) 299*301=299(300+1)=89700+299=8999
Объяснение:
Приравняем числитель и знаменатель к нулю, тогда
x^2-3x-10=0
x^2-6x+5=0. решим эти уравнения любым удобным , для меня это теорема обратная Т.Виета
произведение корней равно минус 10, а сумма равна 3, очевидно это 5 и минус 2, произведение корней равно 5, а сумма 6, очевидно это 5 и 1, и очень хорошо, что есть одинаковые корни. Мы имеем право записать квадратный трехчлен как a(x-x1)*(x-x2), где х1 и х2 это корни квадратного трехчлена, a - коэффициент перед старшей степенью. Тогда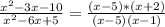 на х-5 можно сократить, окончательно получим.
на х-5 можно сократить, окончательно получим.