Пусть . Понятно, что . Пусть существует натуральное , которое делит и , и . Выберем наибольшее из таких чисел. Тогда делит и разность этих чисел, то есть , но , поскольку и взаимно простые числа. Тогда . Итак, делит и , значит, делит . Следовательно, .
В таком случае, . Понятно, что . Раз , то . Теперь совсем просто: , откуда , что также подходит.
Если указанного значения не существует, то . Но тогда , откуда , что не является простым числом.
Пусть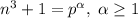 . Понятно, что
. Понятно, что 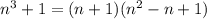 . Пусть существует натуральное
. Пусть существует натуральное 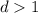 , которое делит и
, которое делит и 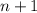 , и
, и 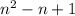 . Выберем наибольшее из таких чисел. Тогда
. Выберем наибольшее из таких чисел. Тогда 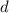 делит и разность этих чисел, то есть
делит и разность этих чисел, то есть 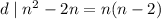 , но
, но 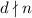 , поскольку
, поскольку 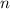 и
и 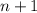 взаимно простые числа. Тогда
взаимно простые числа. Тогда 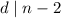 . Итак,
. Итак, 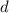 делит
делит 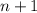 и
и 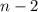 , значит, делит
, значит, делит 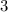 . Следовательно,
. Следовательно, 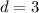 .
.
В таком случае,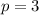 . Понятно, что
. Понятно, что 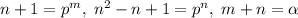 . Раз
. Раз 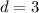 , то
, то 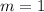 . Теперь совсем просто:
. Теперь совсем просто: 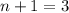 , откуда
, откуда 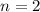 , что также подходит.
, что также подходит.
Если указанного значения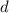 не существует, то
не существует, то 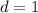 . Но тогда
. Но тогда 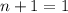 , откуда
, откуда 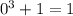 , что не является простым числом.
, что не является простым числом.