абсциссf точки х₀ = 1
Объяснение:
Прежде всего найдем уравнение касательной.
Уравнение касательной имеет вид
Рассмотрим уравнение касательной в точке х₀ (эту точку нам и надо найти)
Для того, чтобы две прямые были параллельны, необходимо, чтобы в уравнениях прямых коэффициенты при х были бы равны.
У прямой у = 2х коэффициент при х равен 2
У касательной коэффициент при х равен
Приравняем коэффициенты и найдем х₀
Проверим.
Подставим х₀ в формулу касательной.
- это уравнение касательной в точке х₀=1.
И эта прямая ║ прямой у = 2х
абсциссf точки х₀ = 1
Объяснение:
Прежде всего найдем уравнение касательной.
Уравнение касательной имеет вид
Рассмотрим уравнение касательной в точке х₀ (эту точку нам и надо найти)
Для того, чтобы две прямые были параллельны, необходимо, чтобы в уравнениях прямых коэффициенты при х были бы равны.
У прямой у = 2х коэффициент при х равен 2
У касательной коэффициент при х равен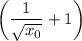
Приравняем коэффициенты и найдем х₀
Проверим.
Подставим х₀ в формулу касательной.
И эта прямая ║ прямой у = 2х