По формуле касательной y=f'(x0)(x-x0) + f(x0)=f'(x0)*x +f(x0)-f'(xo)*xo х0- неизвестная константа точка касания тогда число -3 будет равно f'(xo) надеюсь понятно тк f(x0)-f'(xo)*x0 тоже константа не помноженная на x найдем производную 10x^2+23x+c=0 тк c-константа то получим f'(x)=20x+23 f'(x0)=20x0 + 23=-3 20x0=-26 xo=-13/10 подставим теперь зная что f(x0)-f'(xo)*xo=-8 f(xo)-3*-13/10=8 f(xo)=119/10 теперь подставим х0 в уравнение и приравняем 169/10-23*13/10+с=119/10 откуда 169-23*13+10с=119 10c=119-169+299 x=249/10=24,9
Чтобы вычислить площадь фигуры, ограниченной графиком функции на заданном промежутке , следует найти определенный интеграл:
где — первообразная для функции
1) Имеем функцию и следует вычислить площадь, которую она ограничивает на координатной плоскости на отрезке
Найдем определенный интеграл, приписав перед ним знак "минус", поскольку график функции находится под осью абсцисс:
2) Вычислим площадь фигуры, ограниченной графиками функций и на отрезке
Чтобы найти эту площадь, следует вычислить определенный интеграл разности функций и (только при такой разности площадей, образованных функциями на координатной плоскости, получим площадь фигуры, изображенной на рисунке):
Чтобы вычислить площадь фигуры, ограниченной графиком функции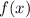 на заданном промежутке
на заданном промежутке ![[a; \ b]](/tpl/images/1350/2276/cd2bf.png) , следует найти определенный интеграл:
, следует найти определенный интеграл:
где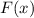 — первообразная для функции
— первообразная для функции 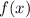
1) Имеем функцию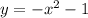 и следует вычислить площадь, которую она ограничивает на координатной плоскости на отрезке
и следует вычислить площадь, которую она ограничивает на координатной плоскости на отрезке ![[1; \ 2]](/tpl/images/1350/2276/2bc6a.png)
Найдем определенный интеграл, приписав перед ним знак "минус", поскольку график функции находится под осью абсцисс:
2) Вычислим площадь фигуры, ограниченной графиками функций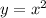 и
и 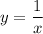 на отрезке
на отрезке ![[1; \ 3]](/tpl/images/1350/2276/24e94.png)
Чтобы найти эту площадь, следует вычислить определенный интеграл разности функций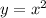 и
и 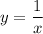 (только при такой разности площадей, образованных функциями на координатной плоскости, получим площадь фигуры, изображенной на рисунке):
(только при такой разности площадей, образованных функциями на координатной плоскости, получим площадь фигуры, изображенной на рисунке):
ответ: 1)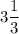 кв. ед.; 2)
кв. ед.; 2) 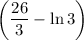 кв. ед.
кв. ед.