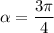Найдем уравнение касательной, проходящей через точку с абсциссой
Для этого найдем производную данной функции:
Найдем значение функции в точке с абсциссой :
Найдем значение производной данной функции в точке с абсциссой :
Уравнение касательной имеет вид:
Подставим значение
Итак, уравнение касательной заданной функции:
Воспользуемся геометрическим смыслом касательной: коэффициент наклона касательной численно равен тангенсу угла наклона с положительным направлением оси
В найденной касательной коэффициент , следовательно, при или
ответ: или
Относительная погрешность равна абсолютной, деленной на приближенное значение, выраженное в процентах.
1.
1) 5,4 = 5. Абс = 5,4-5 = 0,4. Отн = 0,4:5,4*100% = 7,4%
2) 7,9 = 8. Абс = 8-7,9 = 0,1. Отн = 0,1:7,9*100% = 1,27%
3) 1,89 = 2. Абс = 2-1,89 = 0,11. Отн = 0,11:1,89*100% = 5,82%
4) 8,5 = 9. Абс = 9-8,5 = 0,5. Отн = 0,5:8,5*100% = 5,88%
5) 3,71 = 4. Абс = 4-3,71 = 0,29. Отн = 0,29:3,71*100% = 7,82%
6) 11,27 = 11. Абс = 11,27-11 = 0,27. Отн = 0,27:11,27*100% = 2,4%
2.
1) 8,79 = 0. Абс = 9-8,79 = 0,21
2) 0,777 = 0,8. Абс = 0,8-0,777 = 0,023
3) 132 = 130. Абс = 132-130 = 2
4) 1,23 = 1,23. Абс = 1,23-1,23 = 0.
Найдем уравнение касательной, проходящей через точку с абсциссой
Для этого найдем производную данной функции:
Найдем значение функции в точке с абсциссой :
:
Найдем значение производной данной функции в точке с абсциссой :
:
Уравнение касательной имеет вид:
Подставим значение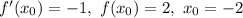
Итак, уравнение касательной заданной функции: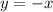
Воспользуемся геометрическим смыслом касательной: коэффициент наклона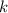 касательной
касательной 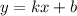 численно равен тангенсу угла наклона
численно равен тангенсу угла наклона 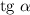 с положительным направлением оси
с положительным направлением оси 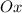
В найденной касательной коэффициент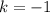 , следовательно,
, следовательно, 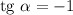 при
при 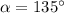 или
или 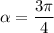
ответ: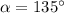 или
или