Алгебра: Найти область определения y=cos5x

Найти область определения y=cos5x

Показать ответ

Ответ:

xovancku

09.07.2020 12:20

1) Решим систему, чтобы облегчить построение:

$\left\{{{4x-3y=12}\atop{2x+2y=1|+*-2}}\right.\\\left\{{{4x-3y=12}\atop{-7y=10}}\right.\\\left\{{{x=\frac{3y+12}{4}}\atop{y=-\frac{10}{7}}}\right.\\\left\{{{x=\frac{3y+12}{4}}\atop{y=-\frac{10}{7}}}\right.\\\left\{{{x=\frac{27}{14}}\atop{y=-\frac{10}{7}}}\right.$

Понимаем, что график не даст нам точные координаты пересечения и строим его схематически (см рис.)

2) Одна точка пересечения (-2; -5) (пересечение прямых x = - 2 и y = -5).

Найдем две точки пересечения:

5x + 2y = 10 и x = -2 ⇒ -10 + 2y = 10 ⇒ y = 10 ⇒ (-2; 10)

5x + 2y = 10 и y = -5 ⇒ 5x - 10 = 10 ⇒ x = 4 ⇒ (4; -5)

Т.к. один из углов треугольника образован пересечением перпендикулярных прямых x = - 2 и y = -5, то он прямоугольный и можем найти длину катетов, вычитая ординаты точек для пары (-2; -5) и (-2; 10) ⇒ a = 10 - (-5) = 15

и абсциссы точек для пары (-2; -5) и (4; -5) ⇒ b = 4 - (-2) = 6

Тогда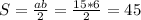 $S=\frac{ab}{2}=\frac{15*6}{2}=45$

Для более общего решения найдем площадь треугольника заданного координатами трех точек в двухмерном декартовом пространстве как половину векторного произведения построенного на двух векторах задающих две стороны треугольника.

Для треугольника построенного на точках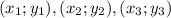 (x_1;y_1),(x_2;y_2),(x_3;y_3) площадь будет равна:

$S=\frac{|(x_1-x_3)*(y_2-y_3)-(x_2-x_3)*(y_1-y_3)|}{2}=\frac{|(-2-4)*(10-(-5))-(-2-4)*(-5-(-5))|}{2}=\frac{|-6*15-(-6)*0|}{2}=\frac{90}{2}=45$

1) постройте прямые в одной системе координат и укажите координаты точки их пересечения. проверьте р

0,0(0 оценок)

Ответ:

baranovdanil2001

27.05.2022 07:08

Какое из выражений больше:
1)√18,
2) 2√6
3) 5
4) √5+√6
1. √18
2. Внесем 2 под знак корня: 2√6=√4*6=√24
3. Найдем, корнем какого числа является 5: 5²=25 => 5=√25
4. Найдем ближайшее целое число, корень из которого является рациональным числом. Это число 4 - √4=2, значит √5 - больше 2, √6 - больше 2, но меньше 2.5, т.к. 2.5²=6.25:
2<√5<2.5; 2<√6<2.5 => √5+√6<5
Если одно из подкоренных выражений больше другого, то корень, извлеченный из этого выражения, больше, чем корень извлеченный из другого выражения, поэтому:
√18<√24
√24<√25
(√5+√6)<√25
ответ: наибольшее из заданных чисел: 5

0,0(0 оценок)

Популярные вопросы: Алгебра