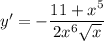Можно по-честному использовать формулу дифференцирования частного двух функций, но, на самом деле, есть путь попроще:
Теперь используем простейшее правило нахождения производной степенной функции
ответ.
Можно по-честному использовать формулу дифференцирования частного двух функций, но, на самом деле, есть путь попроще:
Теперь используем простейшее правило нахождения производной степенной функции
ответ.