Найти промежутки монотонности, точкиэкстремума и экстремумы функции: а) f(х) = 2х3+3х2-2

Показать ответ

Ответ:

Spartak1935

14.02.2021 23:22

1)log0,5(x^2+x)=-1
x^2+x > 0; x(x+1) >0; x < -1 и x > 0

x^2+x = 0,5^(-1)

x^2+x = 2

x^2+x - 2 = 0
x = -2 x = 1

2)2 log3 x=log3 (2x^2-x)

x > 0

2x^2-x >0; x(2x - 1) > 0; x< 0 и х > 0,5
log3 x^2 = log3 (2x^2-x)

x^2 = 2x^2 - x

x^2 - x = 0
x(x-1) = 0

x = 0 x = 1
х = 0 - не подходит
ответ: х = 1

3) 3)log7 (2-x)<=log7 (3x+6)

2-x > 0; x < 2
3x+6 >0; x > -2
2-x <= 3x+6
4x >= -4
x >= -1

[-1;2)

4) log1/2(x^2-4)>log1/2 (x+2)-1
x^2-4 > 0; (x-2)(x+2) >0; x < -2 и x > 2
x + 2 > 0; x > -2
log1/2 (x^2-4)>log1/2 (x+2)-log1/2 1/2
log1/2(x^2-4)>log1/2 2(x+2)
x^2-4 < 2x + 4
x^2 - 2x -8 < 0
(x-4)(x+2) < 0
-2 < x < 4
ответ: (2;4)

5) lg^2x>=9
x > 0
lg^2x - 9 >= 0

(lgx -3)(lgx + 3) >= 0
lgx <= -3 и lgx >= 3
lgx <= lg 10^(-3) lgx >= lg 10^3
x <= 0,001 x >= 1000
ответ: (0;0,001] и [1000;+oo}

0,0(0 оценок)

Ответ:

vika2069

02.02.2021 00:51

Выполнив деление получим:

$\frac{(2x + 3\sqrt{x} - 2)(5\sqrt{x} - 2x + 3)}{(2 + \sqrt{x})(3 - \sqrt{x})} - 4x$

Введём замену. Пусть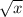 $\sqrt{x}$ = t ≥ 0, тогда x = $t^{2}$ .

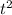Перепишем данное выражение с учётом замены. Получим:

$\frac{(2t^{2} + 3t - 2)(5t - 2t^{2} + 3)}{(2 + t)(3 - t)} - 4x$

Найдём корни всех квадратных трёхчленов в числителе и разложим их на множители:

$2t^{2} + 3t - 2 = 0 \\ D = b^{2} - 4ac = 9 + 16 = 25 \\ x1 = \frac{-3 - 5}{4} = -2 \\ x2 = \frac{-3+5}{4} = 0.5 \\ \\$

Разложение будет иметь вид: 2(t + 2)(t - 0.5)

Аналогично поступаем со вторым:

$-2t^{2} + 5t + 3 = 0 \\ D = b^{2} - 4ac = 25 + 24 = 49 \\ x1 = 3; x2 = -0.5$

Разложение имеет вид: -2(t - 3)(t + 0.5)

Подставим вместо трёхчленов их разложения и проведём некторые преобразования, но оговоримся, что поскольку преобразование идёт лишь при допустимых значениях переменных, то t≥0; t≠3:

$\frac{-4(t+2)(t-0.5)(t-3)(t+0.5)}{(2+t)(3-t)} - 4t^{2} = \frac{-4(t-0.5)(t+0.5)(t-3)}{3-t} - 4t^{2} = \frac{4(t^{2} - 0.25)(3-t)}{3 - t} - 4t^2$ \\ = 4t^{2} - 1 - 4t{2} = -1