(см. объяснение)
Объяснение:
, ОДЗ:
Попробуем решить это уравнение относительно тангенса:
Тогда получили два случая:
или
Применив формулу для тангенса половинного угла, получим:
Применив формулы суммы и разности тангенсов и выполнив очевидные преобразования, получим:
Решим каждое уравнение по отдельности:
1)
2)
Окончательное решение уравнения с учетом ОДЗ:
Найдем теперь корни уравнения, которые удовлетворяют неравенству :
Задание выполнено!
Комментарий:
Замечу, что исходное уравнение можно упростить до вида:
Откуда хорошо видно, что его корень:
Такое решение также является допустимым.
(см. объяснение)
Объяснение:
Попробуем решить это уравнение относительно тангенса:
Тогда получили два случая:
Применив формулу для тангенса половинного угла, получим:
Применив формулы суммы и разности тангенсов и выполнив очевидные преобразования, получим:
Решим каждое уравнение по отдельности:
1)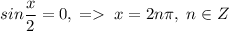
2)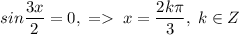
Окончательное решение уравнения с учетом ОДЗ:
Найдем теперь корни уравнения, которые удовлетворяют неравенству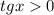 :
:
Задание выполнено!
Комментарий:
Замечу, что исходное уравнение можно упростить до вида:
Откуда хорошо видно, что его корень:
Такое решение также является допустимым.