Объяснение:
Выберем корни уравнения . принадлежащие отрезку
1)
т.к. , то данному неравенству удовлетворяет k=0
2)
данному неравенству удовлетворяет k=1
Объяснение:
Выберем корни уравнения . принадлежащие отрезку![[ 0; 2,5\pi ]](/tpl/images/0942/0183/20233.png)
1)
т.к.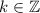
, то данному неравенству удовлетворяет k=0
2)
данному неравенству удовлетворяет k=1