Найти значение выражения:

а)-5 ∙ (-3,6) – 27,8 б)√405√10

2.Найдите корень уравнения:

8 + х3 = х – 5

№3. Найдите значение выражения:

(5-х)х+5х2− 10х +25 при х = 45

№4 Решите неравенство:

а) (х + 5)( х -9) >0 б)(х + 4)(х + 2)(х -10) <0 в)х2 + 2х – 15 ≤ 0

№5. Решить систему:

а){3х−6>0[ х−8>0 б){6−х ≥12х−1 ≥1

Вариант II

1.Найдите значение выражения:

а) – 9 ∙ (-1,3) – 20,1 б) √276√3

2. Найдите корень уравнения:

6 + х4 = х – 9

3.Найдите значения выражения:

(3 – х)х+3х2− 6х+9 при х = 23

№4. Решить неравенства:

а) (х-3)(х-5) >0 б)(х + 7)(х + 5))х – 9) <0 в) 2х2 + 7х – 4 ≤ 0

№5 Решить систему:

а){5х−10<0х+4>0 б) {3−2х ≤5х+6 ≥5

ответ:   1680 деталей .

Объяснение:

За смену токарь должен изготовить 112 деталей.

Пусть токарь должен работать t дней и за эти t дней он должен изготовить всего  х деталей.

Тогда   х=112*t  деталей.

Так как токарь перевыполнял план и изготавливал на 8 деталей за смену больше, то он изготовлял  (112+8)=120 дет. за смену.

И количество дней уменьшилось на 1 и стало равно  (t-1) дней.

Тогда всего токарь изготовил  120(t-1) деталей . Но это количество равно  х .  Получим уравнение:

Токарь должен был работать 15 дней и за каждую смену изготавливать 112 деталей.

Всего он должен изготовить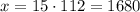     деталей

Ясно, что сторона большого квадрата равна √49=7/см/, и если рассмотреть верхний левый треугольник, в котором гипотенуза АВ равна 5см, введя  переменную х- пусть это будет меньший катет, тода больший катет равен (7-х),по теореме Пифагора

х²+(7-х)²=25; х²+х²-14х+49=25; 2х²-14х+24=0; х²-7х+12=0; По Виета х=3 или х=4, т.е. если один катет 3см, то второй 4см, и наоборот.

А это и есть стороны тех четырех прямоугольников, зная площадь одного, найдя площадь четырех и от площади квадрата отняв полученную площадь, найдем площадь маленького квадрата

Она равна 49-4*4*3=49-48=1/см²/

ответ 1см² , у Вас  это ответ первый.