Число , при котором достигается наибольшее значение, должно удовлетворять паре неравенств: и . Из первого неравенства , из второго , откуда , следовательно, .
При этом наибольшее значение существует: сначала показательная функция больше факториала, однако при достаточно больших значениях (а именно при ) факториал перегоняет, и значения выражения уменьшаются.
Число , при котором достигается наибольшее значение, должно удовлетворять паре неравенств:
, при котором достигается наибольшее значение, должно удовлетворять паре неравенств: 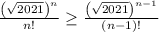 и
и 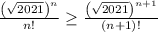 . Из первого неравенства
. Из первого неравенства 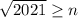 , из второго
, из второго  , откуда
, откуда 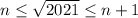 , следовательно,
, следовательно, 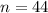 .
.
При этом наибольшее значение существует: сначала показательная функция больше факториала, однако при достаточно больших значениях (а именно при ) факториал перегоняет, и значения выражения уменьшаются.
) факториал перегоняет, и значения выражения уменьшаются.