1)
по формуле у нас все совпдает просто подставляем значения
x=0
2) формула n-го члена для последовательности первых членов 3,5,7,9
формула для n-члена выглядит так:
a1 это первый член
n это номер какого то члена (например 17-ый ; 20-ый)
d это разность то есть на какое число отличается какойто член от предыдущего
у нас известен первый член и несколько последующих
нам нужно только найти d вычтем от друг друга два последовательных члена к примеру 7 и 9 получается 2
значит d=2
Объяснение:
1) 3tg²x+2tgx-1=0
пусть tg=b, тогда:
3b²+2b-1=0
D=b²-4ac=4-4*3*(-1)=4+12=16
b1;2= (-b±√D)/2a= -2±4 / 2*3= -1; 1/3
tgx= 1/3
x= arctg(1/3)+πk
или
tgx= -1
x=arctg(-1)+πk=3π/4+πk
ответ: x=3π/4+пk
(вы допишите что k принадлежит множеству целых чисел, а то мне неудобно 100500 раз писать это.)
2) 14sinxcosx+sin2xcos7x=0 [150°;360°]
7sin2x+sin2xcos7x=0 (использована формула двойного аргумента)
sin2x(7+cos7x)=0
sin2x = 0
2x = πk
x= πk/2
7+cos7x=0
cos7x=-7 не удовлетворяет, т.к. меньше -1 (условие косинуса. значение находится между -1 и 1)
k =0
х =0;
k = 1
х = 90°;
k= 2
х = 180° ;
k = 3
х = 270°;
k = 4
x = 360°
3) 3sin²x+sinxcosx-2cos²x=0
делим на cos²x:
3tg²x+tgx-2=0
если tgx=b, тогда:
3b²+b-2=0
D=b²-4ac=1+4*3*2=25
b1;2= -1±5 / 6= -1; 2/3
tgx= 2/3
x= arctg(2/3)+πk
tgx=-1
x= 3π/4+πk
4) (2sin²x-3sinx +1)√tg=0
2sin²x-3sinx+1=0
sinx=b
2b²-3b+1=0
D=9-8=1
b1;2= (3±1)/4=1/2; 1
sinx= 1/2
x= (-1)^k*π/6+πk
sinx=1
x= π/2+2πk
tgx=0
х=πk
1)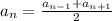
по формуле у нас все совпдает просто подставляем значения
x=0
2) формула n-го члена для последовательности первых членов 3,5,7,9
формула для n-члена выглядит так:
a1 это первый член
n это номер какого то члена (например 17-ый ; 20-ый)
d это разность то есть на какое число отличается какойто член от предыдущего
у нас известен первый член и несколько последующих
нам нужно только найти d вычтем от друг друга два последовательных члена к примеру 7 и 9 получается 2
значит d=2
Объяснение:
1) 3tg²x+2tgx-1=0
пусть tg=b, тогда:
3b²+2b-1=0
D=b²-4ac=4-4*3*(-1)=4+12=16
b1;2= (-b±√D)/2a= -2±4 / 2*3= -1; 1/3
tgx= 1/3
x= arctg(1/3)+πk
или
tgx= -1
x=arctg(-1)+πk=3π/4+πk
ответ: x=3π/4+пk
(вы допишите что k принадлежит множеству целых чисел, а то мне неудобно 100500 раз писать это.)
2) 14sinxcosx+sin2xcos7x=0 [150°;360°]
7sin2x+sin2xcos7x=0 (использована формула двойного аргумента)
sin2x(7+cos7x)=0
sin2x = 0
2x = πk
x= πk/2
или
7+cos7x=0
cos7x=-7 не удовлетворяет, т.к. меньше -1 (условие косинуса. значение находится между -1 и 1)
k =0
х =0;
k = 1
х = 90°;
k= 2
х = 180° ;
k = 3
х = 270°;
k = 4
x = 360°
3) 3sin²x+sinxcosx-2cos²x=0
делим на cos²x:
3tg²x+tgx-2=0
если tgx=b, тогда:
3b²+b-2=0
D=b²-4ac=1+4*3*2=25
b1;2= -1±5 / 6= -1; 2/3
tgx= 2/3
x= arctg(2/3)+πk
или
tgx=-1
x= 3π/4+πk
4) (2sin²x-3sinx +1)√tg=0
2sin²x-3sinx+1=0
sinx=b
2b²-3b+1=0
D=9-8=1
b1;2= (3±1)/4=1/2; 1
sinx= 1/2
x= (-1)^k*π/6+πk
sinx=1
x= π/2+2πk
или
tgx=0
х=πk