В прямоугольном треугольнике гипотенуза будет равна двум медианам, поэтому . Площадь треугольника найдем по формуле , откуда . С другой стороны . По теореме Пифагора . Подставляем c и ab в формулу: . Тогда искомый периметр равен .
Второй :
Возможно было записать две теоремы Пифагора и найти катеты, как:
Тогда .
Здесь предварительно была использована теорема Пифагора для образованного высотой и медианой треугольника:
(см. объяснение)
Объяснение:
Данная задача имеет более одного решения.
Первый :
В прямоугольном треугольнике гипотенуза будет равна двум медианам, поэтому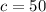
. Площадь треугольника найдем по формуле 
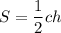, откуда 
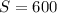. С другой стороны 
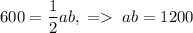. По теореме Пифагора 
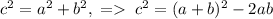. Подставляем c и ab в формулу: 
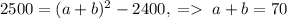. Тогда искомый периметр равен 
.
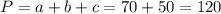Второй :
Возможно было записать две теоремы Пифагора и найти катеты, как:
Тогда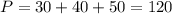
.
Здесь предварительно была использована теорема Пифагора для образованного высотой и медианой треугольника:
Тогда вс длины равны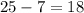
и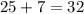 
.
Задача решена!
{2х + 3у = 7
{-5х + 2у = 11
- - - - - - - - - -
Домножим второе уравнение системы на 0,4
{2х + 3у = 7
{-2х + 0,8у = 4,4
Сложим оба уравнения системы
3,8у = 11,4
у = 11,4 : 3,8
у = 3
Подставим значение у в любое уравнение системы
2х + 3 · 3 = 7 или -5х + 2 · 3 = 11
2х + 9 = 7 -5х + 6 = 11
2х = 7 - 9 -5х = 11 - 6
2х = -2 -5х = 5
х = -2 : 2 х = 5 : (-5)
х = -1 х = -1
ответ: (-1; 3).