Обязательная часть.
А1. Какое из чисел НЕ является решением неравенства 4,5 + 3у >0?
Варианты ответов:
1) 0
2) 4,5
3) 3
4) -1,5
ответ: ___
А2. Решите неравенство 6 -7х > 3х – 7:
Варианты ответов:
1) (-∞; 1,3)
2) (0,1; +∞)
3) (-∞; 0,1)
4) (1,3; +∞)
ответ: ___
А3. Сколько целых решений неравенства 2с < -1,3 принадлежит промежутку (-6; 3]?
Варианты ответов:
1) 3
2) 4
3) 5
4) 6
ответ: ___
А4. Какое из приведенных ниже неравенств является верным при любых значениях
х и у, удовлетворяющих условию х > у?
Варианты ответов:
1) у – х > 0
2) у – х < -1
3) х – у > 3
4) х – у > -2
ответ: ___
А5. При каких значениях х значение выражения 6х – 7 больше значения выражения
7х + 8?
Варианты ответов:
1) х < -1
2) х > -1
3) х > -15
4) х < -15
ответ: ___

Дополнительная часть.
В1. Решите неравенство 6х + 3(-5 – 8х) > 2х + 4.
Решение:
ответ:
В2. Решите неравенство методом интервалов: (2,5- х)(2х +3)(х +4) > 0.

Объяснение:

1)Найдите значение функции y= - 2x+4, если значение аргумента равно -6

х= -6

у= -2*(-6)+4=12+4=16

При х= -6 у=16

2) Укажите, для какого значения аргумента значение функции y=4x - 5 равно -4.

у= -4

-4=4х-5

-4х= -5+4

-4х= -1

х= -1/-4

х=0,25

3) Укажите координаты точки пересечения графика функции

у= -0,5х - 5 с осью абсцисс.

График пересекает ось Ох при у=0

у=0

0= -5х-5

5х= -5

х= -1

Координаты точки пересечения графиком оси Ох (-1; 0)

4) Задайте формулой линейную функцию, если известно к = -4 и прямая проходит через точку А(1;5).

y = -4х +9

5= -4*1+9

5=5

5) Графиком какой из данных функций является прямая, проходящая параллельно Ох:

у =1/9

6. Не выполняя построений ,найдите координаты точки пересечения графиков линейных функций у= - 2х-10 и у = 3х-5.

- 2х-10 = 3х-5

-2х-3х= -5+10

-5х=5

х= -1

у=3*(-1)-5

у= -3-5

у= -8

Координаты точки пересечения графиков (-1; -8)

ОДЗ:

Разложим первую скобку в знаменателе на множители. Для этого решим уравнение

Подставим это разложение в исходное выражение и выполним преобразование:

Очевидно, что:

1) выражение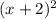 будет всегда положительным при любых x ≠ -2, то есть не влияет на условия неравенства;

2) выражение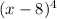 будет неотрицательным при любых x.

Решение исходного неравенства сводится к решению неравенства

с учётом "выколотой" точки x = -2

Имеем две точки: x = -1 и x = 5. Определим знаки последнего выражения на получившихся интервалах:

ответ: