Очень нужно

Выбери числа, которые являются корнями данного квадратного уравнения:

1)-2,5 2) 3) 4)

5)

Показать ответ

Ответ:

3asyavasilkova3

21.04.2022 06:01

1. -15 ≤ 1-2у ≤ 0

2. $4\leq \frac{4}{y} +y\leq 8\frac{1}{2}$

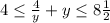
Объяснение:

1. Т.к. в линейном выражении 1-2у перед у стоит знак "-", то при вычислении пределов возможных значений нужно либо поменять направление знаков больше (меньше) либо поменять местами подставляемые значения 1/2 и 8.

для 1/2 ≤ у: 1-2у ≤ 0

для у ≤ 8: 1-2у ≥ -15

Тогда: -15 ≤ 1-2у ≤ 0

2. Здесь перед у знак "+", но появилась нелинейная зависимость 4/у, поэтому нужно вычислить производную функции (4/у + у) и приравнять её к нулю, чтобы найти ее экстремум.

$(\frac{4}{y} +y)'=-\frac{4}{y^2} +1\\-\frac{4}{y^2} +1=0\\y^2=4\\y_1=2; y_2=-2.$

Но так как значение -2 не попадает в наш промежуток по условию, то это значение отбрасываем.

Значит, в точке у=2 имеем экстремум. Определим его значение:

для у=2: $\frac{4}{y} +y=4$ .

На остальных участках функция либо возрастает, либо убывает. подставим граничные значения из условия:

для у=1/2 : $\frac{4}{y} +y=8\frac{1}{2}$

для у=8: $\frac{4}{y} +y=8\frac{1}{2}$ .

Т.е. имеем кривую с максимумами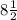 $8\frac{1}{2}$ и минимумом 4.

Тогда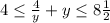 $4\leq \frac{4}{y} +y\leq 8\frac{1}{2}$

0,0(0 оценок)

Ответ:

73487Юлия14271

14.10.2020 11:39

Решение
1) 2cosx-1 < 0
cosx < 1/2
arccos(1/2) + 2πn < x < 2π - arccos(1/2) + 2πn, n ∈ Z
π/3 + 2πn < x < 2π - π/3 + 2πn, n ∈ Z
π/3 + 2πn < x < 5π/3 + 2πn, n ∈ Z
2) sin2x - √2/2 < 0
sin2x < √2/2
- π - arcsin(√2/2) + 2πk < 2x < arcsin(√2/2) + 2πk, k ∈ Z
- π - π/4 + 2πk < 2x < π/4 + 2πk, k ∈ Z
- 5π/4 + 2πk < 2x < π/4 + 2πk, k ∈ Z
- 5π/8 + πk < x < π/8 + πk, k ∈ Z
3) tgx<1
- π/2 + πn < x < arctg(1) + πn, n ∈ Z
- π/2 + πn < x < π/4 + πn, n ∈ Z

0,0(0 оценок)

Популярные вопросы: Алгебра