Округлите 3,525 до десятых и найдите абсолютную и относительную погрешность​

1 этап составление математической модели
Пусть первоначальная цена куртки равна х руб,
тогда  цена куртки после снижения её на 20% составила (1-0,2)*х=0,8х руб,
а после дальнейшего повышения на 10% составила 0,8х*(1+0,1)=0,8х*1,1=0,88х руб.
По условию, разница между первоначальной ценой и последней составила 180 руб.
Составляем уравнение:
х - 0,88х =180

2 этап работа с математической моделью (решение уравнения)
0,12х =180
х=180:0,12
х=1500 

3 этап ответ на вопрос задачи
Получили х=1500 руб. - составила первоначальная цена куртки

ответ: 1500 руб.

Определим общее число расстановок на пяти позициях 5 шариков:

Однако, среди этих расстановок есть недопустимые (то есть те, при которых между зеленым и желтым шариком располагаются два или более шарика). Найдем число недопустимых расстановок.

Найдем число недопустимых размещений зеленого и желтого шарика. Их можно просто перечислить:

1) зеленый на 1-ом месте, желтый на 4-ом месте

2) зеленый на 1-ом месте, желтый на 5-ом месте

3) зеленый на 2-ом месте, желтый на 5-ом месте

4) зеленый на 4-ом месте, желтый на 1-ом месте

5) зеленый на 5-ом месте, желтый на 1-ом месте

6) зеленый на 5-ом месте, желтый на 1-ом месте

В каждом из этих случаев оставшиеся три шарика могут размещаться на свободных местах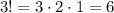

Таким образом, всего имеется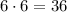 недопустимых расстановок.

Значит, допустимых расстановок имеется:

ответ: 84