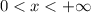Необходимое условие сходимости выполняется только при
Поскольку а при ряд сходится по радикальному признаку Коши:
то заданный ряд сходится по признаку сравнения при
Таким образом, область сходимости заданного ряда:
ответ:
Необходимое условие сходимости выполняется только при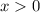
Поскольку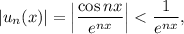 а при
а при 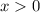 ряд
ряд 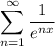 сходится по радикальному признаку Коши:
сходится по радикальному признаку Коши:
то заданный ряд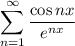 сходится по признаку сравнения при
сходится по признаку сравнения при 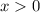
Таким образом, область сходимости заданного ряда: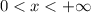
ответ: