По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется
По второму признаку Лейбница предел ряда должен стремится к 0.
Второе условие Лейбница выполняется. Таким образом, рассматриваемый ряд сходится. Исследуем на абсолютной и условной сходимости ряда. Для этого возьмём исходный ряд по модулю
По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется
По второму признаку Лейбница предел ряда должен стремится к 0.
Второе условие Лейбница выполняется. Таким образом, рассматриваемый ряд сходится. Исследуем на абсолютной и условной сходимости ряда. Для этого возьмём исходный ряд по модулю
Этот ряд расходится, так как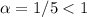 .
.
Следовательно, исследуемый ряд сходится условно.