Перевод: Два самолета в одно время вылетели из аэродрома, один из них полетел на запад, а второй на юг. Через 2 часа полёта они были на расстоянии 2000 км друг от друга. Если скорость одного самолета равна 75% скорости второго самолета, то найдите скорости этих самолетов.
Решение. Обозначим скорость второго самолета через x (км/ч). Тогда скорость первого самолета равна 0,75·x (км/ч).
Расстояние S, которого пролетел самолёт определяется через скорость υ и время t по формуле: S=υ·t.
Пусть самолёты в одно время вылетели из аэродрома O (см. рисунок). Один из них полетел на запад и через 2 часа достиг точку B. Тогда расстояние от точки O до точки B определим на основе данных υ₁=0,75·x (км/ч) и t=2 часа: OB=S₁=υ₁·t=0,75·x·2=1,5·x.
Второй полетел на юг и через 2 часа достиг точку A. Тогда расстояние от точки O до точки A определим на основе данных υ₂=x (км/ч) и t=2 часа, OA=S₂=υ₂·t=x·2=2·x.
Так как направления движений самолётов перпендикулярны, то получаем прямоугольный треугольник AOB, в котором:
∠O=90°, AO=2·x и OB=1,5·x - катеты, а AB - гипотенуза, равная 2000 км.
Для прямоугольного треугольника AOB верна теорема Пифагора:
AB²=AO²+OB².
Тогда
2000²=(2·x)²+(1,5·x)² или 4·x²+2,25·x²=4000000 или
6,25·x²=4000000 или x²=4000000:6,25 или x²=640000.
Отсюда, так как в нашем случае скорость положительная, то скорость второго самолета x=800 км/ч, а скорость первого самолета равна 0,75·800=600 км/ч.
Дана функция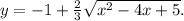
Начнём с выражения под корнем.
Минимум по производной равен: 2х - 4 = 0, х = 2.
Под корнем 4 - 4*2 + 5 = 1.
Минимум всей функции равен -1 +(2/3)*1 = -1/3.
Перенесём -1 влево и возведём обе части уравнения в квадрат.
(у + 1)² = (4/9)(x² - 4x + 5).
В правой части выделим полный квадрат.
x² - 4x + 5 = (x² - 4x + 4) - 4 + 5 = (x - 2)² + 1.
Правая часть примет вид (4/9)((x - 2)² + 1) = (4/9)(x - 2)² + (4/9).
Перенесём квадрат с х влево:
(у + 1)² - (4/9)(x - 2)² = 4/9.
Разделим обе части на 4/9.
((у + 1)²)/(4/9) - ((x - 2)²/1) = 1.
Получили уравнение гиперболы, повёрнутой на 90 градусов.
Но в соответствии с заданием, только верхняя часть этой гиперболы удовлетворяет заданному уравнению.
600 км/ч, 800 км/ч
Объяснение:
Перевод: Два самолета в одно время вылетели из аэродрома, один из них полетел на запад, а второй на юг. Через 2 часа полёта они были на расстоянии 2000 км друг от друга. Если скорость одного самолета равна 75% скорости второго самолета, то найдите скорости этих самолетов.
Решение. Обозначим скорость второго самолета через x (км/ч). Тогда скорость первого самолета равна 0,75·x (км/ч).
Расстояние S, которого пролетел самолёт определяется через скорость υ и время t по формуле: S=υ·t.
Пусть самолёты в одно время вылетели из аэродрома O (см. рисунок). Один из них полетел на запад и через 2 часа достиг точку B. Тогда расстояние от точки O до точки B определим на основе данных υ₁=0,75·x (км/ч) и t=2 часа: OB=S₁=υ₁·t=0,75·x·2=1,5·x.
Второй полетел на юг и через 2 часа достиг точку A. Тогда расстояние от точки O до точки A определим на основе данных υ₂=x (км/ч) и t=2 часа, OA=S₂=υ₂·t=x·2=2·x.
Так как направления движений самолётов перпендикулярны, то получаем прямоугольный треугольник AOB, в котором:
∠O=90°, AO=2·x и OB=1,5·x - катеты, а AB - гипотенуза, равная 2000 км.
Для прямоугольного треугольника AOB верна теорема Пифагора:
AB²=AO²+OB².
Тогда
2000²=(2·x)²+(1,5·x)² или 4·x²+2,25·x²=4000000 или
6,25·x²=4000000 или x²=4000000:6,25 или x²=640000.
Отсюда, так как в нашем случае скорость положительная, то скорость второго самолета x=800 км/ч, а скорость первого самолета равна 0,75·800=600 км/ч.