Определите истинность следующих утверждений. функция y = x2 − 14x + 50 имеет наименьшее значение. верно или нет функция y = x2 − 14x + 50 определена только для положительных значений аргумента. верно или нет функция y = x2 − 14x + 50 возрастает на промежутке [7; +∞) верно или нет функция y = x2 − 14x + 50 имеет нули при двух значениях аргумента. верно или нет
верно
Функция y = x² − 14x + 50 определена только для положительных значений аргумента.
неверно, у определена для всех х
Функция y = x² − 14x + 50 возрастает на промежутке [7;+∞)
верно
Функция y = x² − 14x + 50 имеет нули при двух значениях аргумента
неверно
y=х²-14х+50= (x-7)²+1 не имеет нулей
1) Функция y = x² - 14x + 50 имеет наименьшее значение. Верно или нет?
Да, верно. Так как ветви направлены вверх, то точка вершины параболы достигает своего наименьшего значения.
2) Функция y = x2 − 14x + 50 определена только для положительных значений аргумента. верно или нет?
Нет, не верно. Данную функцию можно представить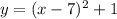 , что само собой показывает что для действительных х функция определена.
, что само собой показывает что для действительных х функция определена.
3) Функция y = x2 − 14x + 50 возрастает на промежутке [7;+∞) верно или нет?
Да, так как координата абсцисса вершины х: x = -b/2a = 14/2 = 7 и, зная, что ветви параболы направлены вверх, то функция возрастает на промежутке [7;+∞).
Функция y = x2 − 14x + 50 имеет нули при двух значениях аргумента. верно или нет?
Нет, не верно. Так как вершина параболы y = (x-7)² + 1 имеет координаты (7;1)и ,очевидно, что вершина находится выше оси абсциссы, то с прямой y=0 квадратичная функция общих точек не имеет.