Находим производную.
Приравниваем производную к нулю.
Теперь найдём знак производной на каждом промежутке.
- +
------------------------------------------------------> x
Функция возрастает там, где производная положительна, и убывает, где она отрицательна.
ответ: функция убывает при ; возрастает при .
Одна точка экстремума: .
Находим производную.
Приравниваем производную к нулю.
Теперь найдём знак производной на каждом промежутке.
- +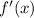
----------------------------- -------------------------> x
-------------------------> x
Функция возрастает там, где производная положительна, и убывает, где она отрицательна.
ответ: функция убывает при![x\in\left(-\infty;\ -3,5]](/tpl/images/1745/1225/b67ee.png) ; возрастает при
; возрастает при 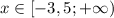 .
.
Одна точка экстремума: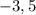 .
.