Число 3 располагается ближе к числу , чем число 2, так как
Рассмотрим числа и . Зарисуем схематично числа 3 и 2 и отметим их синусы. Обе эти величины положительны. Но поскольку число 3 расположено ближе к числу , то его синус меньше.
Число 3 располагается ближе к числу , чем число 4, так как
Рассмотрим числа и . Зарисуем схематично числа 3 и 4 и отметим их косинусы. Числа 3 и 4 лежат в левой полуплоскости, поэтому их косинусы отрицательны. Поскольку число 3 расположено ближе к числу , то его косинус меньше.
Возьмем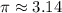
Число 3 располагается ближе к числу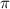
, чем число 2, так как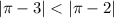 
Рассмотрим числа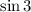
и 
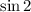. Зарисуем схематично числа 3 и 2 и отметим их синусы. Обе эти величины положительны. Но поскольку число 3 расположено ближе к числу 
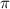, то его синус меньше.
Число 3 располагается ближе к числу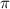
, чем число 4, так как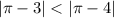 
Рассмотрим числа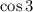
и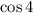 
. Зарисуем схематично числа 3 и 4 и отметим их косинусы. Числа 3 и 4 лежат в левой полуплоскости, поэтому их косинусы отрицательны. Поскольку число 3 расположено ближе к числу 
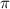, то его косинус меньше.
Тогда итоговая цепочка принимает вид:
1.
6sin^2x-3sinx*cosx-cos^2x=sin^2x+cos^2x
5sin^2x-3sinx*cosx-2cos^2x=0 /:cos^2x≠0
5tg^2x-3tgx-2=0
замена tgx=t
5t^2-3t-2=0
t=1
t=-2/5
обратная замена:
1) tgx=1
x=pi/4+pik, k∈Z
2) tgx=-2/5
x=-arctg(2/5)+pik, k∈Z
pi/4+pik, k∈Z
-arctg(2/5)+pik, k∈Z
2.
5sin^2x+3sinx*cosx-2cos^2x=3sin^2x+3cos^2x
2sin^2x+3sinx*cosx-5cos^2x=0 /:cos^2x≠0
2tg^2x+3tgx-5=0
замена tgx=t
2t^2+3t-5=0
t=1
t=-5/2
обратная замена:
1) tgx=1
x=pi/4+pik, k∈Z
2) tgx=-5/2
x=-arctg(5/2)+pik, k∈Z
pi/4+pik, k∈Z
-arctg(5/2)+pik, k∈Z