Однажды весной я пошла гулять к озеру .погода была чудесная и на душе было легко и радостно.вдруг я заметила лягушку.она прыгнула на листик,затем на камень и в камыши.я её больше не видела.я села на берегу и смотрела на закат.небо было то ли розовое,то ли жёлтое,фиолетовое.на до мною пролетела ворона,села рядом , совсем близко, на веточку.я долго на неё смотрела , а потом она улетела полетела куда то за облако и скрылась.время было позднее и я пошла домой.иду по тропинке и рядом зайчик скачет,такой пушистый и весёлый.я присела что бы его погладить,он сначала испугался,отпрыгнул,а потом с небольшой опаской приблизился ко мне и я его погладила.на этом мои приключения у озера закончились!
Объяснение:
1) Приводишь к общему знаменателю и при этом выполняется:
6х - 1 ≠ 0
х ≠ 1/6
(x+2)(6x-1) = 15
6x^2-x+12x-2-15 = 0
6x^2+11x-17 = 0
D = b^2-4ac
D = 11^2-4*6*(-17) = 121+408 = 529
x1 = (-b+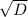
)/2a = (-11+23)/2*6 = 12/12 = 1
x2 = (-b-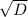
)/2a = (-11-23)/2*6 = -34/12 = -17/6
ответ: 1; -17/6
2) Чтобы найти точку пересечения двух графиков достаточно их приравнять и решить уравнение, т.е.:
2/x = x-1
2/x - x + 1 = 0
-x^2+x+2 = 0 Домножим на (-1):
x^2 -x -2 =0
по т. Виета:
x1+x2 = 1
x1*x2 = -2
x1= 2 x2= -1
Если x = 2, то у = 1
Если х = -1, то у = -2
ответ: (2;1) и (-1;-2)